2023.04.14 - [Programming/특성 공학] - [Machine Learning]지도 학습에서 언급했듯이 모델 파라미터 즉, 매개변수의 종류는 다양합니다. 그래서 이번 포스트에서는 지도 학습의 종류에 대하여 알아보도록 하겠습니다.
먼저, 지도학습에는 분류(Classification)와 회귀(Regression)가 있습니다.
먼저 분류는 가능성 있는 여러 클래스 레이블(label) 중 하나를 예측 하는 것입니다. 이전 장 붓꽃 예제를 살펴보면 3가지 붓꽃의 품종 중 하나를 데이터( feature )를 이용해 예측하였습니다.
이때 두 개만 분류 하는 것을 이진 분류(binary classification)와 셋 이상의 클래스로 분류하는 다중 분류(multiclass classification)가 있습니다.
분류 Classification
이진 분류(Binary Classification)
단순히 말해 이진 분류는 Yes / No 로만 나올 수 있도록 하는 것입니다. 예를 들어보면 "당신은 비만인가요?"에 대한 답이겠네요.
이 때 양성 클래스와 음성 클래스로 분류됩니다. (양성이라고 해서 무조건 좋은 것은 아닙니다.)
"당신은 비만인가요?"에 대한 질문의 답으로 개발자가 원하는 값이, 즉 학습하고자 하는 대상이 비만이라면 '비만'이라는 값이면 '비만'이 양성이 됩니다.
반대로 비만이 아닌 값은 '음성'이 되겠네요
다중 분류(Multiclass Classification)
이진 분류와 다르게 다중 분류는 3개 이상의 결과가 나오는 것을 의미합니다
다중 분류는 이전 장에서 해봤던 붓꽃 예제가 이에 해당됩니다. 다른 예를 들자면 환자들의 각종 상태를 분석해 병명을 예측하는 것도 다중 분류에 해당되겠네요.
회귀 Regression
회귀는 보통 연속적인 숫자, 또는 부동 소수점 수(실수)를 예측합니다.
옥수수 농장의 전년도 수확량과 날씨, 고용 인원수 등으로 올해 수확량을 예측하거나 교육 수준, 나이, 주거지 등을 바탕으로 연간 소득을 예측하는 등등 어떤 숫자 된 결과물이 될 수 있을 때 이를 회귀라고 이야기합니다.
분류와 회귀 구분하기
분류와 회귀를 구분하는 방법은 출력값에 연속성이 있는지를 확인해 보면 됩니다.
연소득을 예측했을 때 이 사람의 연소득이 40,000,000원으로 예측되어야 한다고 한다면
40,000,001원이거나 39,999,999이라고 예측해도 예측한 양은 차이가 약간은 있지만 그렇게 큰 차이는 아니기 때문에 별다른 문제가 되진 않을 것입니다.
반대로 분류는 비만도를 구해 이 사람이 비만인지 과체중인지 저체중인지 등등 확실하게 그 결과가 정해져야 할 때를 의미하게 됩니다.
정리를 해보자면!
결과가 Yes / No 또는 이미 정해진 결과대로 예측이 되어야 하는 경우는 분류를 사용,
여러 연속적인 숫자가 예측되어서 허용한 오차 범위 내에 값이 있어도 될 때는 회귀를 사용한다고 보면 됩니다.
일반화 Generalization
훈련 데이터를 여러 개 준비해서 훈련된(학습된) 모델이 처음 보는 데이터가 주어져도 정확하게 예측할 수 있으면 이를 일반화되었다고 합니다.
보통 훈련 데이터 세트를 준비해 머신러닝을 시키게 되면, 보통이면 훈련 세트에 대해 정확히 예측하도록 모델을 구축합니다. 훈련 세트와 테스트 세트가 매우 비슷하다면 여러분이 만들어 놓은 모델은 테스트 세트에서도 정확하게 예측할 것이라 기대합니다.
이때 주의 해야 할 상황 중 하나는 아주 복잡한 모델 만든다면 훈련세트에만 정확한 모델이 되어 버릴 수가 있습니다.
여기서 복잡한 모델이란 너무나 많은 분류 데이터들을 사용하는 경우입니다. 예를 하나 들어 볼까요?
| 나이 | 이름 | 성별 | 혼인상태 | 자녀수 | 차량 구매 여부 |
| 25 | 김유정 | 남자 | 미혼 | 0 | no |
| 45 | 박미영 | 여자 | 기혼 | 2 | yes |
| 23 | 김경진 | 여자 | 미혼 | 0 | no |
| 34 | 박철수 | 남자 | 기혼 | 1 | yes |
| 44 | 손맹구 | 남자 | 미혼 | 0 | yes |
| 39 | 강유리 | 여자 | 이혼 | 1 | yes |
과대 적합 Overfitting & 과소 적합 Underfitting
한 회사의 고객 데이터라고 예시를 들어 보았습니다. 위 회사에서는 자동차 구매를 위해 고객들에게 전화를 할까 하는데, 기존에 자동차를 구매하지 않았던 고객들에게는 구매를 추천해 주지 않기( 전화를 하지 않겠죠? )로 합니다.
따라서 위의 데이터를 분석하여 구매했던 사람들을 분석해야 할 것 같습니다.
먼저 규칙을 한번 찾아보겠습니다. 이 규칙이 바로 구매하지 않은 사람과 구매 한 사람을 분류하는 기준이 될 것입니다.
- 나이 분류 : 30대 이상인 사람들이 구매했다.
- 이름 분류 : 성이 김 씨인 사람들은 구매하지 않았다.
- 혼인 분류 : 미혼인 사람들은 대부분 구매하지 않았지만, 40대 이상인 남자는 구매했다.
- 자녀 분류 : 자녀가 있으면 차를 대부분 구매했다.
"결과적으로 나이가 30대이고, 성이 김 씨가 아니며, 혼인을 한 사람들은 대부분 우리 회사 차량을 살 것이다."라는 결론을 내렸습니다.
일단 위와 같은 기준으로 모델을 만들었다고 생각해 보면 100% 정확하게 맞아 들어가는 규칙을 정의한 것 같습니다. 하지만 사실상 위의 규칙 말고도 데이터를 만족할 만한 규칙은 얼마든지 만들어 낼 수 있습니다. 나이가 45, 34, 44, 39인 사람들이 구매했다. 같은 규칙 같은 것들이죠
아무튼 기존 데이터셋에 딱 들어맞는 규칙은 얼마든지 만들어 낼 수 있습니다. 하지만 이게 저희가 원하는 결과일까요??
답은 NONO! 왜냐하면 우리는 이 데이터에 존재하는 고객들에 대한 답은 이미 알고 있고, 더해서 새로운 고객이 차량을 구매할 것 인가 이기 때문입니다.
따라서 새로운 고객에도 잘 작동하는 규칙을 찾아야만 하며, 이미 준비된 훈련 세트에서 100% 정확도를 달성하는 것은 크게 도움이 되지 않습니다.
다시 일반화에 대한 이야기를 해보겠습니다. 일반화란, 우리가 만들어 놓은 규칙(모델)이 새로운 데이터에도 적절하게 예측할 수 있는 상태를 의미하는데, 어떻게 하면 될까요?
바로 간단한 모델을 만드는 것입니다. 간단한 모델일수록 일반화가 더 잘 될 것이라는 뜻인데, 예를 들어 위의 예제에서는 "30대 이상의 사람들은 차량을 구매하려고 한다."라고 규칙을 세우는 것이 좋을 것 같네요.
이렇게 규칙을 만들게 되면 모든 고객데이터를 만족할 뿐만 아니라, 나이 외에 혼인 상태, 자녀 수 등을 추가한 것보다 더 신뢰할 수 있을 것 같습니다.
하지만 바로 이전에 여러 가지 규칙을 사용해 너무 복잡한 모델을 만드는 바람에 새로운 데이터에 대해 예측이 어렵게 만드는 것을 과대적합이라고 합니다.
반대로 "김 씨가 아니면 모두 차량을 구매할 것이다."와 같이 데이터의 면면과 다양성을 잡아내지 못하는 규칙을 적용하는 것을 과소적합이라고 합니다.
정리를 해보자면!
- 과대적합은 규칙이 너무 많고 복잡해지기 때문에 민감해져 일반화가 어렵습니다.
- 과소적합은 규칙이 적용되는 범위가 너무 넓어 모델의 신뢰도가 떨어집니다.
우리는 과소적합과 과대적합에 대한 절충점을 찾아야 할 것입니다. 보통은 데이터의 양이 데이터의 다양성을 키워주게 됩니다. 한마디로 데이터가 많을수록 더 적절하게 복잡하고 신뢰성 있는 모델을 만들 수 있게 도와준 다는 것이죠
본격적으로 지도 학습에 대하여 예제를 통하여 설명해 보도록 하겠습니다!
예제를 위한 데이터셋 준비 1 - forge [이진 분류]
먼저 아주 단순한 두 개의 특성만을 가지고 있는 forge 데이터셋을 준비해 보겠습니다. 이진 분류 데이터셋이며 산점도로 데이터의 분포를 먼저 확인해 보겠습니다.
#사용 할 라이브리 임포트하기
from IPython.display import display
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import mglearn
plt.rcParams['axes.unicode_minus'] = False
import platform
path = 'c:/Windows/Fonts/malgun.ttf'
from matplotlib import font_manager, rc
if platform.system() == 'Darwin':
rc('font', family='AppleGothic')
elif platform.system() == 'Windows':
font_name = font_manager.FontProperties(fname=path).get_name()
rc('font', family=font_name)
else:
print('Unknown system... sorry!')# mglearn에서 forge datasets 가져오기
# 기본은 np.darray 로 되어있는데, pandas로 데이터를 다루기 위해 변환
X, y = mglearn.datasets.make_forge()
forge_data = []
for item_X, item_y in zip(X, y):
forge_data.append(np.append(item_X, item_y))
# forge datasets를 pandas의 데이터 프레임으로 변환
forge_df = pd.DataFrame(columns=["특성1", "특성2", "분류"], data=forge_data)
forge_df.head()
mglearn.discrete_scatter(forge_df["특성1"], forge_df["특성2"], forge_df["분류"]) #Parameter : x축 데이터, y축 데이터, 사용할 분류
plt.legend(["클래스 1", "클래스 2"], loc=4)
plt.xlabel("첫 번째 특성")
plt.ylabel("두 번째 특성")
plt.show()
print("forge 데이터셋의 특성들의 모양 : {}".format(forge_df[['특성1','특성2']].shape)) #특성의 모양 확인forge 데이터셋의 특성들의 모양 : (26, 2)
DataFrame의 데이터 모양을 확인해 보니 26개의 데이터 포인트와 2개의 특성을 갖는 것을 확인할 수 있습니다. 다음은 회귀 알고리즘 설명을 위한 데이터셋입니다.
예제를 위한 데이터셋 준비 2 - wave [ 저차원 회귀 알고리즘 ]
마찬가지로 인위적으로 만든 데이터셋이며 입력 특성 한 개와(분석해야 할 특성)과 모델링할 타깃 변수 ( 맞춰야 할 값 - 응답 ) 하나를 갖습니다.
X, y = mglearn.datasets.make_wave(n_samples=40)
wave_data = []
for item_X, item_y in zip(X, y):
wave_data.append(np.append(item_X, item_y))
# forge datasets를 pandas의 데이터 프레임으로 변환
wave_df = pd.DataFrame(columns=["입력 특성", "타깃(응답)"], data=wave_data)
wave_df.head()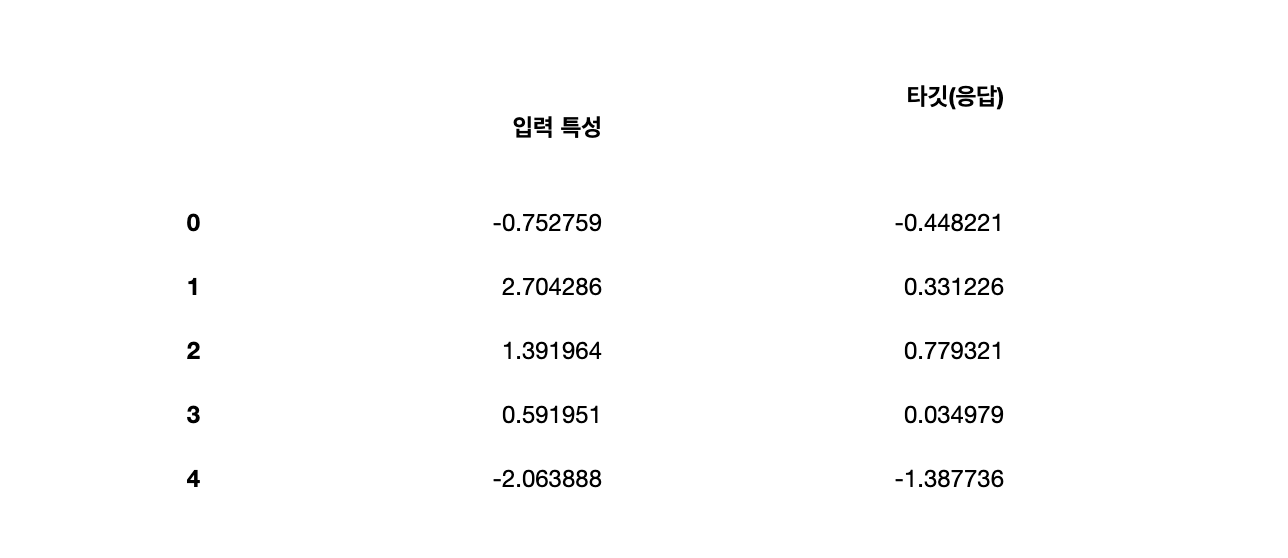
plt.plot(wave_df['입력 특성'], wave_df['타깃(응답)'], 'o')
plt.ylim(-3, 3)
plt.xlabel("특성")
plt.ylabel("타깃")Text(0,0.5, '타깃')
매우 매우 단순한 데이터 셋입니다. 회귀에 대해서 간단히 설명하자면
1) 입력된 특성들을 이용해
2) 타깃 값을 예측
위의 두 단계라고 볼 수 있습니다. 추후에 각종 회귀에 대해 이야기하겠지만 먼저 데모 데이터셋인 wave 데이터셋은 매우 특성이 적은 저차원 데이터셋이라고 할 수 있습니다. 단순히 2차원 공간에 표현하기 쉽기 때문에 선택하였습니다.
물론 우리가 저차원 데이터셋인 wave 데이터셋을 통해 얻어낸 인사이트가 특성이 매우 많은 고차원 데이터셋에서 그대로 유지가 되지 않을 수도 있습니다만, 각종 회귀 알고리즘을 배우기 위해서 사용할 것이다라고 생각 하시면 됩니다.
wave 같은 저차원 데이터셋을 사용해서 회기 알고리즘 공부를 하고, 이어서 실제 연구 결과로 이루어진 데이터셋도 두 가지를 사용해 보겠습니다.
예제를 위한 데이터셋 준비 3 - 위스콘신 유방암 데이터셋 breast_cancer [ 고차원 분류 알고리즘 ]
실제 위스콘신 대학에서 유방암 종양의 임상 데이터를 기록해 놓은 데이터 셋입니다. 타깃은 유방암 데이터셋 ( 입력 특성 )을 이용해 각 종양을 구분합니다.
breast_cancer 데이터셋은 유방암 데이터셋이 입력 특성이 되고, 이에 따른 종양의 종류(타깃)는 다음과 같이 구분됩니다.
- benign(양성) - 해롭지 않은 종양
- malignant(악성) - 암 종양
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
print("cancer.keys(): \n{}".format(cancer.keys()))
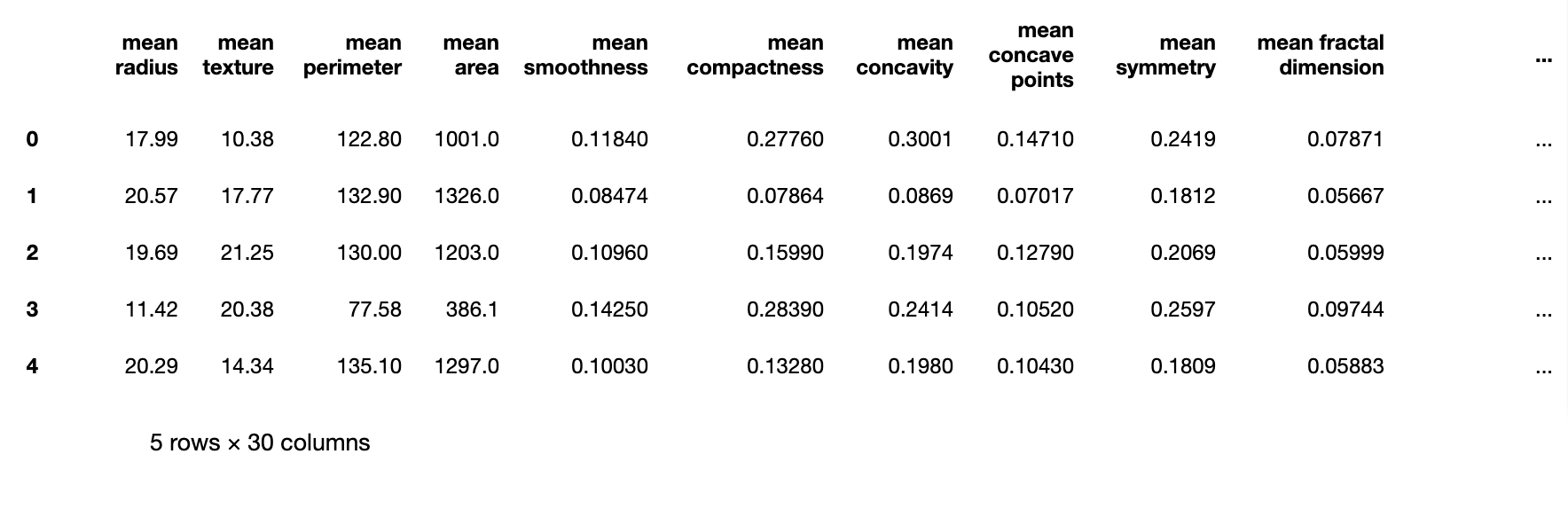
cancer_features_df = pd.DataFrame(data=cancer.data, columns=cancer.feature_names)
cancer_target_df = pd.DataFrame(data=cancer.target, columns=["result"])
cancer_features_df.head()
cancer.keys():
dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names'])
cancer_target_df.head()
cancer_df = pd.merge(cancer_features_df, cancer_target_df, right_index=True, left_index=True)
cancer_df.head()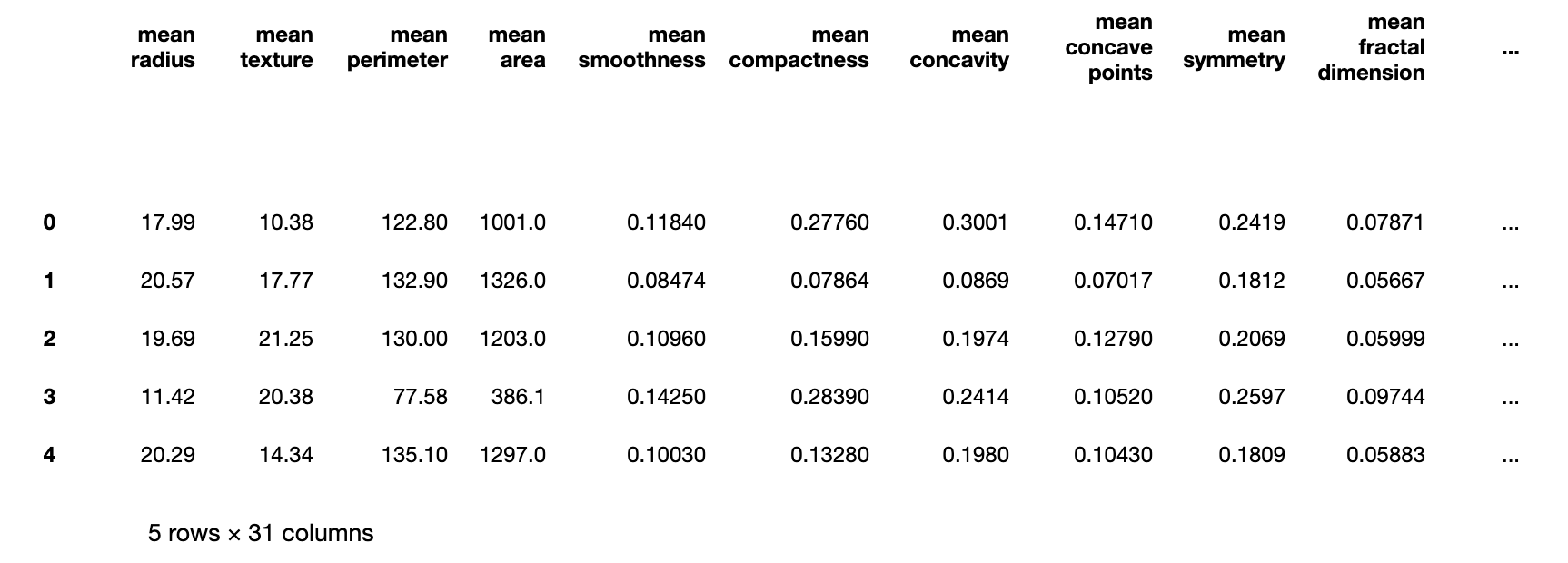
pandas를 이용해 데이터 프레임으로 만들어 보았습니다. 제일 마지막 칼럼인 result 칼럼은 타깃이 되고, 나머지 칼럼들이 입력 특성이 됩니다.
각 타깃 별 개수를 확인해 보도록 하겠습니다.
print("클래스 별 샘플 개수:\n{}".format({n: v for n, v in zip(cancer.target_names, np.bincount(cancer.target))}))클래스 별 샘플 개수:
{'malignant': 212, 'benign': 357}
양성 종양이 357개, 악성 종양이 212개가 있네요!
예제를 위한 데이터셋 준비 4 - 보스턴 주택가격 boston, extended_boston [ 고차원 회귀 알고리즘 ]
위스콘신 유방암 데이터셋과 마찬가지로 1970년 보스턴 주택 가격을 범죄율, 찰스강 인접도, 고속도로 접근성 등의 정보를 이용해 예측합니다.
from sklearn.datasets import load_boston
boston = load_boston()
print("데이터의 형태 : {}".format(boston.data.shape))
boston_features_df = pd.DataFrame(data=boston.data, columns=boston.feature_names)
boston_target_df = pd.DataFrame(data=boston.target, columns=["result"])
boston_df = pd.merge(boston_features_df, boston_target_df, right_index=True, left_index=True)
boston_df.head()데이터의 형태 : (506, 13)
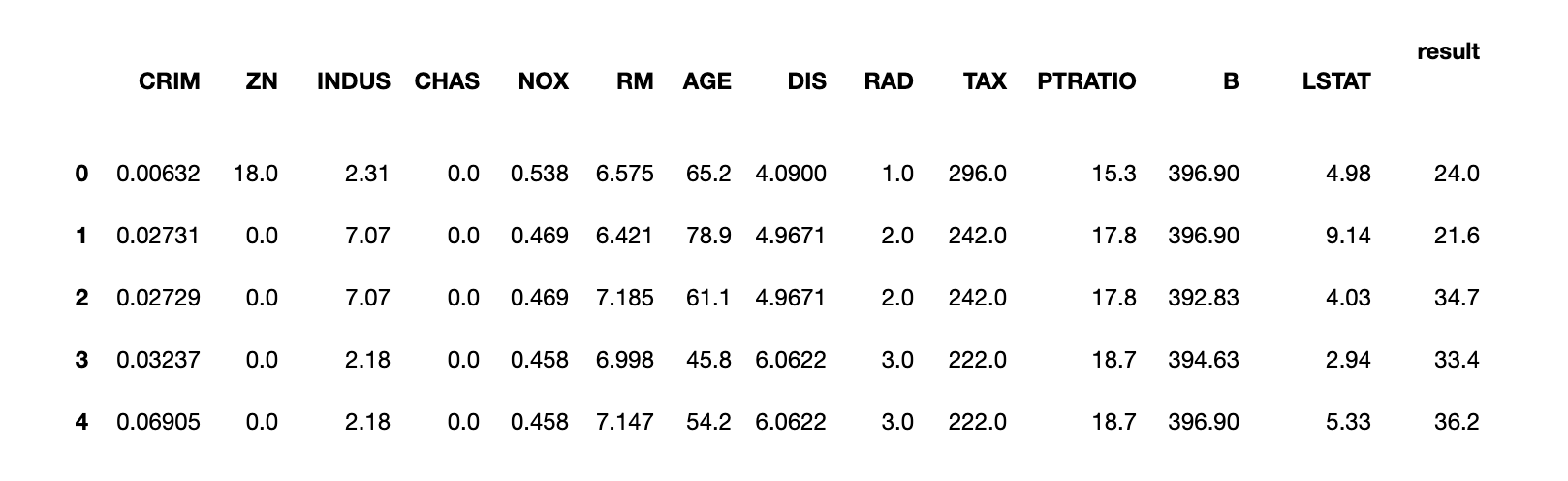
먼저 확인된 boston 데이터셋의 입력 특성의 개수는 13개, 데이터셋의 갯수는 506개가 있는 것이 확인됩니다.
하지만 위의 13개 입력 특성뿐만 아니라, 특성끼리의 상호작용이 발생하기 때문에 특성끼리 곱하여 의도적으로 확장한 데이터셋(extended_boston)을 사용할 겁니다.
예를 들어 범죄율, 고속도로의 개별 특성뿐만 아니라 범죄율과 고속도로의 접근성의 상호작용( 곱 )도 개별적인 특성으로 생각하겠다는 이야기입니다.
이것처럼 특성을 유도해 내는 것을 특성 공학(feature engineering)이라고 합니다. 특성 공학에 대해서는 추후 간단히 설명하겠습니다.
X, y = mglearn.datasets.load_extended_boston()
print("X.shape: {}".format(X.shape))X.shape: (506, 104)
13개의 원래 특성에 2개씩 짝지은 91개의 데이터셋이 추가되어 총 104개의 데이터셋이 된 것을 확인할 수 있습니다.
앞으로 여러 머신러닝 알고리즘들의 특성들을 보여주고 설명하기 위해 위의 데이터셋들을 사용할 것입니다.
'Programming > 특성 공학' 카테고리의 다른 글
| [Machine Learning] 선형 회귀 (0) | 2023.05.02 |
|---|---|
| [Machine Learning] 최근접 이웃(K-NN) (0) | 2023.04.24 |
| [Machine Learning]지도 학습 (0) | 2023.04.14 |
| [데이터 전처리]수치 변환 (1) | 2023.04.04 |
| [Machine Learning]일변량 통계 (0) | 2023.03.28 |