이번 포스팅에서는 데이터 특성을 표현하기 위한 구간 분할(bining) or 이산화, 그리고 상호작용과 다항식에 대하여 알아보도록 하겠습니다.
아주 폭넓게 사용하는 선형 모델과 트리 기반 모델들은 특성의 표현 방식으로 인해 미치는 영향이 매우 다릅니다. "파이썬 라이브러리를 활용한 머신러닝"책 2장에서 사용된 wave 데이터셋을 사용하겠습니다. 이 데이터셋은 입력 특성이 하나뿐입니다. 이 데이터셋을 이용해 선형 회귀모델과 결정 트리 회귀를 비교해 보겠습니다.
from IPython.display import display
import numpy as np
import matplotlib.pyplot as plt
import mglearn
import platform
plt.rcParams['axes.unicode_minus'] = False
%matplotlib inline
path = 'c:/Windows/Fonts/malgun.ttf'
from matplotlib import font_manager, rc
if platform.system() == 'Darwin':
rc('font', family='AppleGothic')
elif platform.system() == 'Windows':
font_name = font_manager.FontProperties(fname=path).get_name()
rc('font', family=font_name)
else:
print('Unknown system... sorry~~~~~')
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
X, y = mglearn.datasets.make_wave(n_samples=100)
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)
reg = DecisionTreeRegressor(min_samples_split=3).fit(X, y)
plt.plot(line, reg.predict(line), label="결정 트리")
reg = LinearRegression().fit(X, y)
plt.plot(line, reg.predict(line), '--' , label="선형 회귀")
plt.plot(X[:, 0], y, 'o', c='k')
plt.ylabel("회귀 출력")
plt.xlabel("입력 특성")
plt.legend(loc='best')
plt.show()
구간 분할
선형 모델은 선형 관계로만 모델링하므로 특성이 하나일 땐 직선으로 나타냅니다. 결정 트리는 이 데이터로 훨씬 더 복잡한 모델을 만들어 내는 것이 확인됩니다.
그러나 이는 데이터 표현 방식에 따라 굉장히 달라지게 되는데, 연속형 데이터에 아주 강력한 선형 모델을 만드는 방법 중 하나는 한 특성을 여러 특성으로 나누는 구간 분할 bining입니다.(이산화라고도 합니다.)
np.linspace로 만들어낸 입력값 범위( -3 ~ 3 )가 일정하기 나뉘어 여러 구간으로, 예를 들면 10개로 되어 있다고 생각해 보겠습니다. 그럼 각 데이터 포인트가 어떤 구간에 속하는지로 나타낼 수 있습니다. 이렇게 하려면 먼저 구간을 정해야 합니다. -3과 3 사이에 일정한 간격으로 10개의 구간을 정의하겠습니다.
np.linspace 함수를 이용해 11개의 지점을 만들어 10개 구간을 만들겠습니다.
bins = np.linspace(-3, 3, 11)
print("구간: {}".format(bins))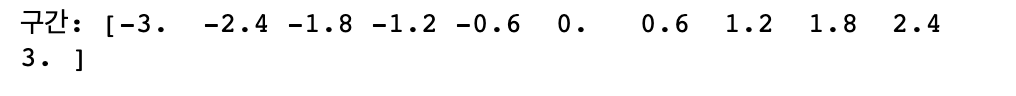
첫 번째 구간은 -3부터 -2.4 사이의 데이터 값을 담습니다. 두 번째 구가는 -2.4부터 -1.8 사이인 모든 데이터 포인트를 포함합니다.
그다음 각 데이터 포인트가 어느 구간에 속하는지 기록합니다. np.digitize 함수를 사용하면 간단하게 계산할 수 있습니다.
which_bin = np.digitize(X, bins=bins)
print('\n데이터 포인트:\n', X[:5])
print('\n데이터 포인트의 소속구간:\n', which_bin[:5])
위의 코드를 이용해 wave 데이터셋에 있는 연속형 특성을 각 데이터 포인트가 어느 구간에 속했는지로 인코딩한 범주형 특성으로 바뀌었습니다. 이 데이터에 scikit-learn의 preprocessing 모듈에 있는 OneHotEncoder로 이산적인 이 특성을 원-핫-인코딩으로 변환하겠습니다.
OneHotEncoder는 pandas.get_dummies와 같지만 현재는 숫자로 된 범주형 변수에만 적용시킬 수 있습니다.
from sklearn.preprocessing import OneHotEncoder
#OneHotEncoder를 사용
encoder = OneHotEncoder(sparse=False) # 희소행렬 형태로 나타내지 않음(각 아이템의 위치값을 나타내지 않음)
#encoder.fit은 which_bin에 나타낸 유일한 값을 찾습니다.
encoder.fit(which_bin)
#One-hot-encoding으로 변환
X_binned = encoder.transform(which_bin)
print(X_binned[:5])
구간이 10개로 구성되었기 때문에 변환된 데이터셋 X_binned는 10개의 특성으로 구성됩니다.
print("X_binned.shape: {}".format(X_binned.shape))
One-Hot-Encoding 된 데이터로 선형 회귀 모델과 결정 트리모델을 다시 만들어 표현해 보겠습니다.
line_binned = encoder.transform(np.digitize(line, bins=bins))
reg = LinearRegression().fit(X_binned, y)
plt.plot(line, reg.predict(line_binned), label='구간 선형 회귀')
reg = DecisionTreeRegressor(min_samples_split=3).fit(X_binned, y)
plt.plot(line, reg.predict(line_binned), '--', label='구간 결정 트리')
plt.plot(X[:, 0], y, 'o', c='k')
plt.vlines(bins, -3, 3, linewidth=1, alpha=.2)
plt.legend(loc='best')
plt.ylabel('회귀 출력')
plt.xlabel('입력 특성')
plt.show()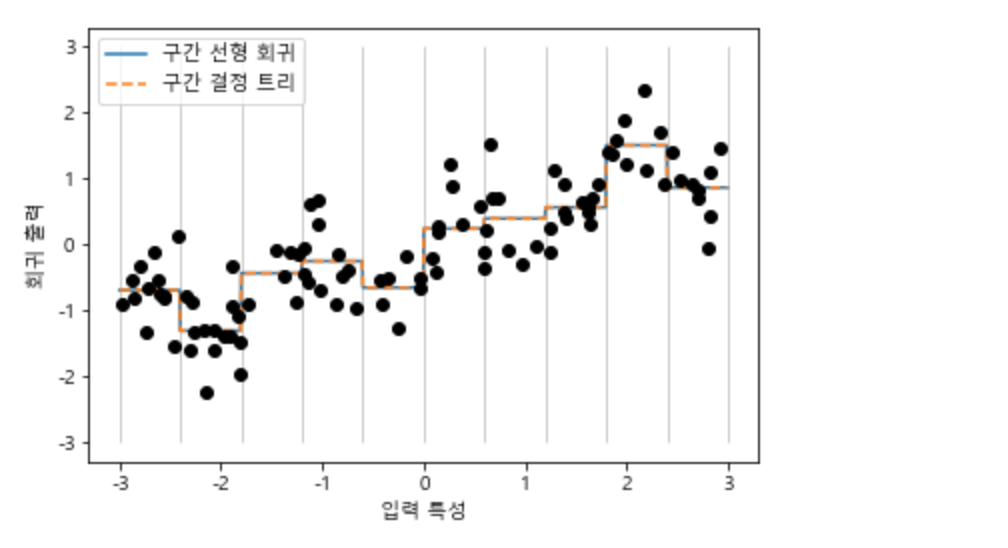
선형 회귀와 결정트리가 완벽하게 겹쳐져 있는 것이 확인됩니다. 구간별로 이 두 모델이 예측한 것은 상숫값입니다. 즉 "이 구간에서의 값은 이거야"라고 하는 것과 같습니다. 따라서 각 구간 안에서는 특성의 값이 상수이므로, 어떤 모델이든 그 구간의 포인트에 대해서는 같은 값을 예측할 것입니다.
구간으로 나눈 특성을 사용하기 전과 비교해 보면, 결정 트리는 기존보다 모델이 단순해졌고, 선형 모델은 조금 복잡해진 것으로 확인됩니다.
트리 모델은 데이터를 애초에 자유롭게 나눠서 학습하기 때문에 특성의 값을 구간으로 나누는 것이 별 도움은 되지 않습니다. 다르게 생각해 보면 결정 트리는 데이터셋에서 예측을 위한 가장 좋은 구간을 학습한다고 볼 수 있습니다. 거기다가 구간 나누기는 특성마다 따로 해야 하지만, 결정 트리는 한 번에 여러 특성을 살펴볼 수 있습니다. 하지만 선형 모델은 구간 나누기를 통해 큰 이득을 보았습니다.
일부 특성과 출력이 비선형 관계이지만, 용량이 매우 크고 고차원 데이터셋이라 선형 모델을 사용해야 한다면 구간 분할이 모델 성능을 높이는데 아주 좋은 방법이 될 수 있습니다.
상호작용과 다항식
특별히 특성을 다양하게 나타내게 하는 방법은 원본 데이터에 상호작용 interaction과 다항식 polynomial을 추가하는 방법입니다. 이런 종류의 특성 공학은 통계적 모델링에서 자주 사용하지만 일반적인 머신러닝 애플리케이션에서도 많이 사용됩니다.
구간 분할을 통해 배웠었던 내용 중 선형 모델이 wave 데이터셋의 각 구간에 대해 상숫값을 학습한 것이 확인되었습니다. 그런데 선형모델은 이러한 절편만 학습하는 것이 아닌 구간별로 기울기도 학습할 수 있습니다.
선형 모델에 기울기를 추가하는 방법은 구간으로 분할된 데이터에 원래 특성을 그대로 다시 추가하는 것입니다. 이렇게 하면 11차원 (10개 구간에 대한 특성을 새로이 추가) 데이터셋이 만들어지게 됩니다.
X_combined = np.hstack([X, X_binned]) # hstack을 이용해 구간별 One-hot-encoding된 데이터 추가
print(X_combined.shape)
reg = LinearRegression().fit(X_combined, y)
line_combined = np.hstack([line, line_binned]) # 예측할 선에 대해서도 One-Hot-Encoding된 데이터를 추가함
plt.plot(line, reg.predict(line_combined), label='원본 특성을 더한 선형 회귀')
for bin in bins:
plt.plot([bin, bin], [-3, 3], ':', c='k', linewidth=1) #x축은 각 구간(bin, bin), y축은 -3 부터 3까지 표현
plt.legend(loc='best')
plt.ylabel('회귀 출력')
plt.xlabel('입력 특성')
plt.plot(X[:, 0], y, 'o', c='k')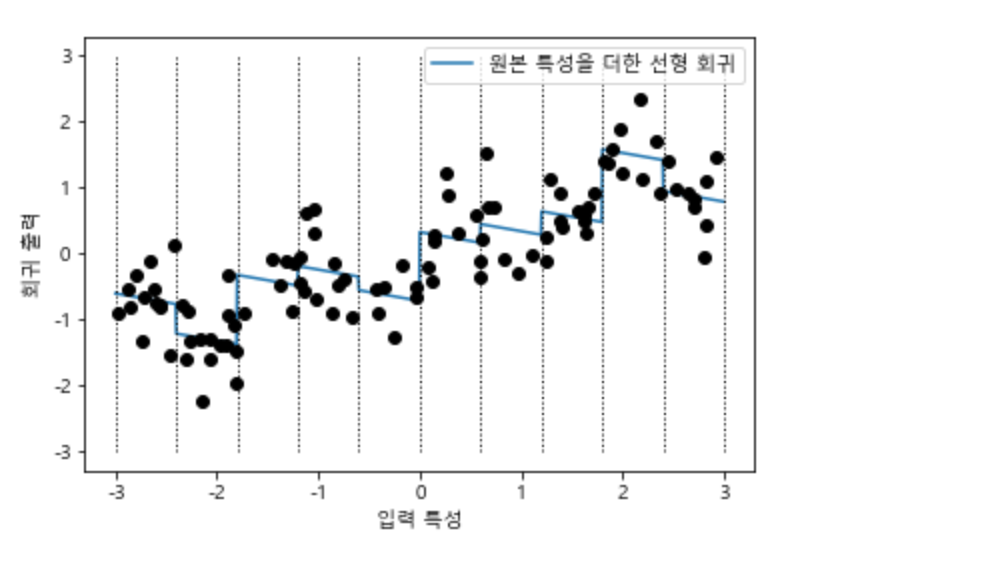
이 모델은 각 구간의 절편과 기울기를 학습하였습니다. 학습한 기울기는 음수이고, 모든 구간에 걸쳐서 모든 기울기가 동일합니다. 즉 x축 특성이 하나이므로 기울기도 하나입니다.
기울기가 모든 구간에서 동일하다 보니 별로 유용해 보이지는 않습니다. 오히려 각 구간에서 다른 기울기는 가지는 게 좋을 것 같네요.
이런 효과를 위해서 데이터 포인트가 있는 구간과 x 축 사이의 상호작용 특성을 추가할 수도 있습니다. 이 특성이 구간 특성과 원본 특성의 곱입니다.
X_product = np.hstack([X_binned, X * X_binned]) # 인코딩된 구간데이터와, 구간과 원본 특성의 곱을 구한 데이터를 추가적으로 합침
print(X_product.shape)
위 데이터셋은 이제 데이터 포인트가 속한 구간과 이 구간에 원본 특성을 곱한 값을 더해 총 20개의 특성을 가지게 되었습니다. 이 곱셈 특성을 각 구간에 대한 x축 특성의 복사본이라고 생각할 수 있습니다. 즉 이 값은 구간 안에서는 원본 특성이고 다른 곳에서는 0입니다.
새롭게 만들어낸 데이터 포인트를 이용해 선형 모델을 적용시켜 보겠습니다.
reg = LinearRegression().fit(X_product, y)
line_product = np.hstack([line_binned, line * line_binned]) # 예측해야 할 데이터도 훈련한 데이터와 같이 상호작용을 구함
plt.plot(line, reg.predict(line_product), label='원본 특성을 곱한 선형 회귀')
for bin in bins:
plt.plot([bin, bin], [-3, 3], ':', c='k', linewidth=1)
plt.plot(X[:, 0], y, 'o', c='k')
plt.ylabel('회귀 출력')
plt.xlabel('입력 특성')
plt.legend(loc='best')
plt.show()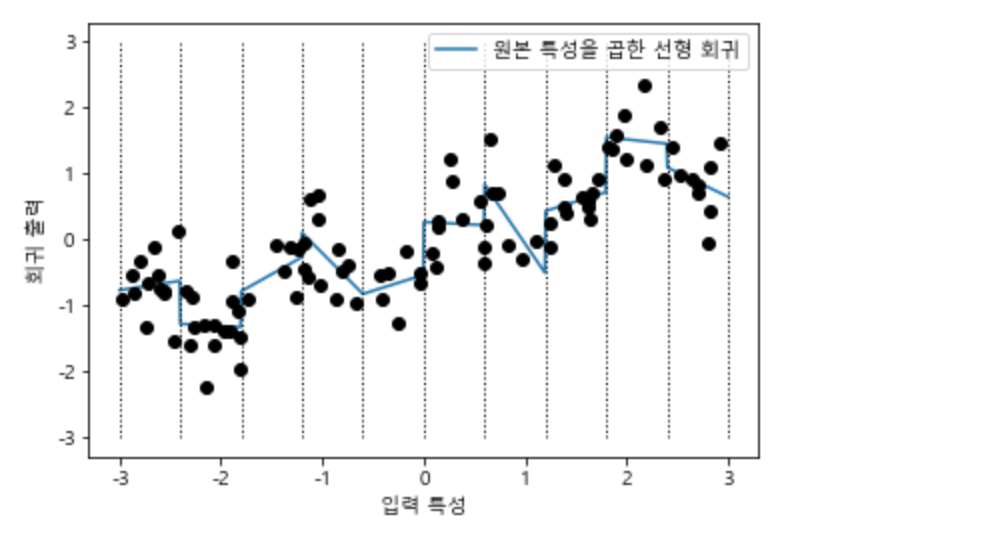
원본 특성의 다항식 추가하기
위의 그림에서 알아볼 수 있듯이 이 모델에서는 각 구간에서의 절편과 기울기가 모두 달라지게 되었습니다.
구간 나누기는 연속형 특성을 확장하는 방법 중 하나입니다. 원본 특성의 다항식을 추가하는 방법도 있습니다. 예를 들어 특성 x가 주어지면 이 특성에 대한 제곱값, 세제곱값, 네 제곱값 등을 새롭게 추가하는 것을 시도해 볼 수 있습니다. preprocessing 모듈의 PolynomialFeatures에 구현되어 있습니다.
from sklearn.preprocessing import PolynomialFeatures
# x ** 10 까지의 고차항을 추가합니다.
# 기본값인 "include_bias=True"는 절편을 위해 값이 1인 특성을 추가합니다.
poly = PolynomialFeatures(degree=10, include_bias=False)
poly.fit(X)
X_poly = poly.transform(X)10차원을 사용했기 때문에 10개의 특성이 새로 만들어집니다. include_bias를 True로 설정하면 절편까지 고려하여 11개의 특성이 만들어집니다.
print('X_poly.shape: {}'.format(X_poly.shape))
X와 X_poly의 값을 비교해 보겠습니다.
print('X 원소:\n{}'.format(X[:5]))
print('X_poly 원소:\n{}'.format(X_poly[:5]))
각 특성의 차수를 알려주는 get_features_names 메소드를 사용해 특성의 의미를 파악할 수 있습니다.
print('항 이름:\n{}'.format(poly.get_feature_names()))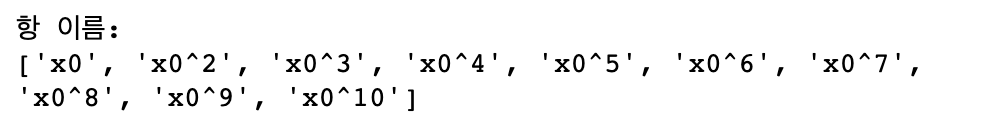
X_poly의 첫 번째 열은 X와 같고 다른 열은 첫 번째 열의 각 거듭제곱입니다. 그래서 어떤 값은 매우 크게 나오는 것이 확인됩니다.
다항식 특성을 선형 모델과 함께 사용하면 전형적인 다항 회귀 polynormial regression 모델이 됩니다.
reg = LinearRegression().fit(X_poly, y)
line_poly = poly.transform(line)
plt.plot(line, reg.predict(line_poly), label='다항 선형 회귀')
plt.plot(X[:, 0], y, 'o', c='k')
plt.ylabel('회귀 출력')
plt.xlabel('입력 특성')
plt.legend(loc='best')
plt.show()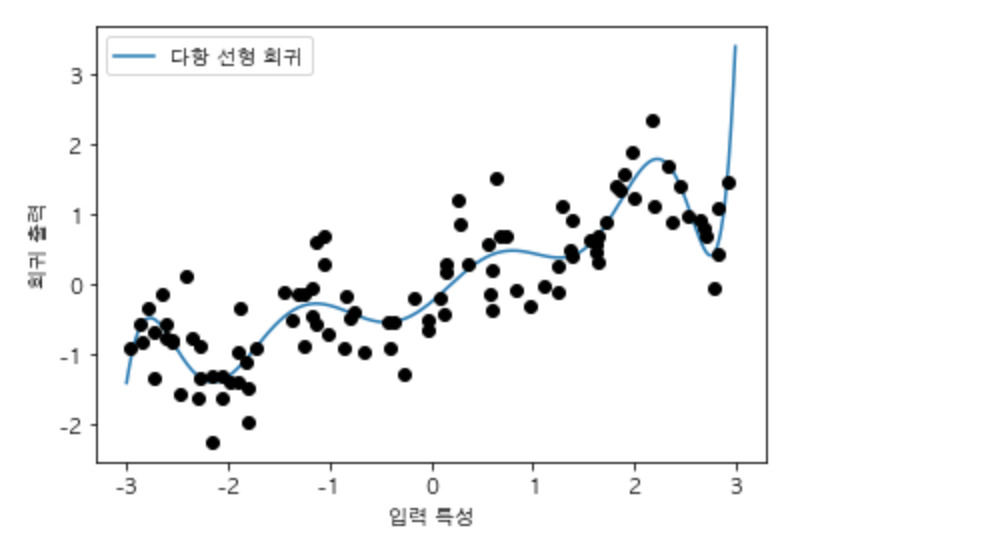
다항식 특성은 1차원 데이터셋임에도 불구하고 매우 부드러운 곡선을 만들어 내는 것이 확인됩니다. 그러나 고차원 다항식은 데이터가 부족한 영역에서 너무 민감하게 작용하여 기울기가 급격하게 바뀌는 것이 확인됩니다.
비교를 위해 커널 SVM과 비교해 보겠습니다. 아무런 변환도 거치지 않은 원본 데이터를 학습시켜 보겠습니다.
from sklearn.svm import SVR
for gamma in [1, 10]:
svr = SVR(gamma=gamma).fit(X, y)
plt.plot(line, svr.predict(line), label='SVR gamma={}'.format(gamma))
plt.plot(X[:, 0], y, 'o', c='k')
plt.ylabel('회귀 출력')
plt.xlabel('입력 특성')
plt.legend(loc='best')
plt.show()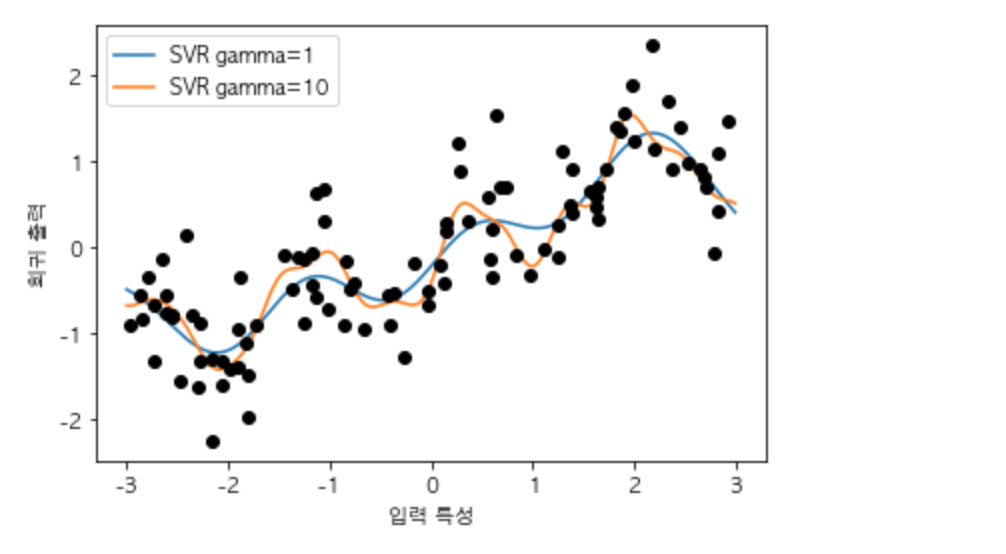
비교적 훨씬 복잡한 커널 SVM을 사용해 특성 데이터를 변환하지 않고 다항 회귀와 비슷한 복잡도를 가진 예측을 만들어 냈습니다.
조금 더 현실적인 차이를 보기 위해 보스턴 주택가격 데이터셋을 이용해 보도럭 하겠습니다. 이때 사용할 데이터셋은 확장된 형태의 데이터셋이 아닌, 어떠한 특성 공학도 들어가지 않은 데이터셋을 사용해 보겠습니다.
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
boston = load_boston()
X_train, X_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=0)
# 데이터 스케일 조정하기
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)이어서 차수를 2로 하여 다항식 특성을 마련합니다.
poly = PolynomialFeatures(degree=2).fit(X_train_scaled)
X_train_poly = poly.transform(X_train_scaled)
X_test_poly = poly.transform(X_test_scaled)
print('X_train.shape: {}'.format(X_train.shape))
print('X_train_poly.shape: {}'.format(X_train_poly.shape))
이 데이터에는 원래 특성이 13개인데 105개의 교차 특성으로 확장되었습니다. 새로운 특성은 원래 특성의 제곱은 물론 가능한 두 토성의 조합을 모두 포함합니다. 즉 degree=2로 하면 원본 특성에서 두 개를 뽑아 만들 수 있는 모든 곱을 얻어 낼 수 있습니다.
어떤 원본 특성이 곱해져 새 특성이 만들어졌는지 확인하기 위해 get_feature_names 메소드를 사용해 보겠습니다.
print("다항 특성 이름:\n{}".format(poly.get_feature_names()))
첫 번째 특성은 상수항으로써 단순히 일정한 절편을 나타내기 위해 추가된 항입니다. 그다음 13개 특성은 원본특성입니다. 그다음은 원본 특성의 제곱항과 첫 번째 특성과 다른 특성 간의 조합입니다.
상호작용 특성이 있는 데이터와 없는 데이터에 대해 Ridge를 사용해 성능을 비교해 보겠습니다.
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train_scaled, y_train)
print('상호작용 특성이 없을 때 점수: {:.3f}'.format(ridge.score(X_test_scaled, y_test)))
ridge = Ridge().fit(X_train_poly, y_train)
print('상호작용 특성이 있을 때 점수: {:.3f}'.format(ridge.score(X_test_poly, y_test)))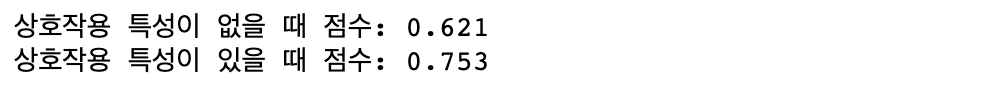
상호작용 특성이 있을 때 Ridge의 성능을 크게 높인 것이 확인됩니다. 하지만 랜덤 포레스트 같이 더 복잡한 모델을 사용하면 이야기가 달라집니다.
from sklearn.ensemble import RandomForestRegressor
rf = RandomForestRegressor(n_estimators=100, random_state=0).fit(X_train_scaled, y_train)
print("상호작용 특성이 없을 때 점수 : {:.3f}".format(rf.score(X_test_scaled, y_test)))
rf = RandomForestRegressor(n_estimators=100, random_state=0).fit(X_train_poly, y_train)
print("상호작용 특성이 있을 때 점수 : {:.3f}".format(rf.score(X_test_poly, y_test)))
특성을 추가하지 않아도 랜덤 포레스트는 Ridge의 성능과 비슷합니다. 오히려 상호작용과 다항식을 추가하면 성능이 줄어듭니다.
지금까지 데이터 특성을 표현하기 위한 구간 분할(bining) or 이산화, 그리고 상호작용과 다항식 표현 방법을 통하여 데이터의 전처리하는 방법을 알아보며 모델 성능을 높이는 과정을 분석해 보았습니다!
다음 포스팅에서는 일변량 통계에 대하여 알아보도록 하겠습니다.
'Programming > 특성 공학' 카테고리의 다른 글
| [Machine Learning]지도 학습 (0) | 2023.04.14 |
|---|---|
| [데이터 전처리]수치 변환 (1) | 2023.04.04 |
| [Machine Learning]일변량 통계 (0) | 2023.03.28 |
| [데이터 전처리]연속형과 범주형 (One Hot Encoding) (0) | 2023.03.16 |
| [데이터 전처리]정규화(Normalisation)와 스케일 조정 (0) | 2021.04.07 |