이번 블로그부터는 역전파 시리즈를 시작해 보도록 하겠습니다!
오차역전파법을 수식으로 이해하기 위해서는 미분의 연쇄법칙에 대해서 먼저 이야기해봐야 합니다. 계산 그래프를 통한 이해에도 연쇄법칙을 알고 들어가야 하기 때문에, 먼저 미분의 연쇄법칙부터 살펴보겠습니다.
합성 함수
함수 𝑦=𝑓(𝑢)의 𝑢가 𝑔(𝑥)라면 𝑦=𝑓(𝑔(𝑥))라고 중첩해서 표현이 가능합니다. 이때 중첩 함수 𝑓(𝑔(𝑥))를 함수 𝑓(𝑢)와 𝑔(𝑥)의 합성 함수라고 합니다. 예를 들어 함수 𝑧=(2−𝑦)2) 2은𝑢=2−𝑦와 함수 𝑧=𝑢2의 합성 함수라고 할 수 있습니다. 신경망에서의 예를 들어보면
에서 출력 함수 𝑦는 𝑥1,𝑥2,...𝑥𝑛의 1차함수 𝑓와 활성화 함수 𝑎의 합성 함수라고 볼 수 있겠습니다. 𝑧=𝑓(𝑥1,𝑥2,...,𝑥𝑛)=𝑤1𝑥1+𝑤2𝑥2+...+𝑤𝑛𝑥𝑛+𝑏𝑦=𝑎(𝑧) 즉 다음과 같은 상황을 그려볼 수 있겠네요.
1) 데이터 입력 𝑥1,𝑥2,...,𝑥𝑛
2) 가중 입력 𝑧=𝑓(𝑥1,𝑥2,...,𝑥𝑛)=𝑤1𝑥1+𝑤2𝑥2+...+𝑤𝑛𝑥𝑛+𝑏
3) 출력 𝑦=𝑎(𝑧) 일
변수 함수의 연쇄법칙
함수 𝑦=𝑓(𝑢)의 변수 𝑢가 일변수 𝑢=𝑔(𝑥)일 때, 합성함수 𝑓(𝑔(𝑥))의 도함수(미분)는 다음과 같이 정의할 수 있습니다.
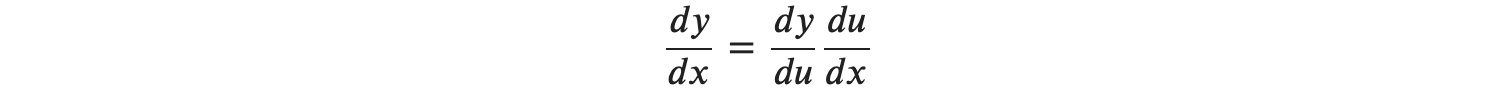
위 식을 합성 함수의 미분공식이라고 볼 수 있습니다. 또한 이를 연쇄 법칙 - chain rule이라고도 합니다. 위 식을 토대로 살펴보면𝑥가 변화 했을 때 𝑦의 변화량을 구하기 위해
- 𝑢의 변화량에 대한 𝑦의 변화량을 구하고
- 𝑥의 변화량에 대한 𝑢의 변화량을 구해서 곱한다
또한 𝑑𝑥, 𝑑𝑦, 𝑑𝑢를 하나의 변수로 놓고 생각해 봤을 때 좌변은 우변의 𝑑𝑢를 약분한 것입니다. 따라서 합성함수의 미분은 분수처럼 약분할 수 있다고 생각할 수 있겠네요. 이 규칙을 토대로 𝑦가 𝑢의 함수, 𝑢가 𝑣의 함수, 𝑣가 𝑥의 함수일 때, 𝑑𝑦𝑑𝑥는 다음과 같습니다.
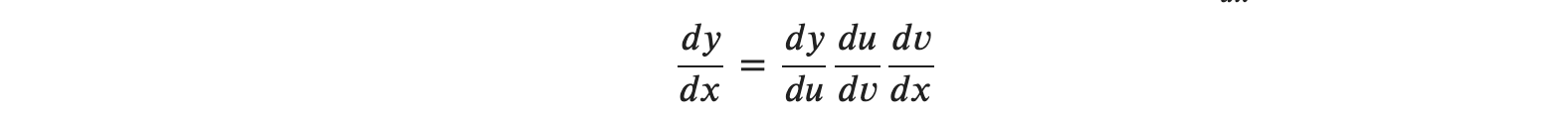
또 다른 예를 들어 보겠습니다. 시그모이드 함수와 다른 함수를 합성해서 가정해 볼 텐데요 예를 들어 다음과 같은 식이 있다고 가정합니다.
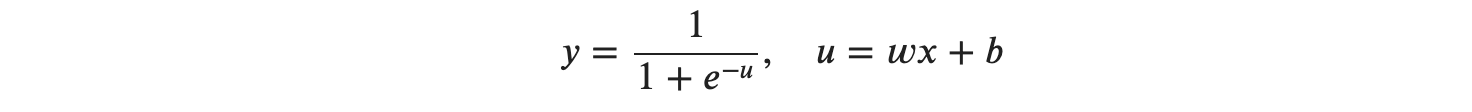
y는 시그모이드 함수이므로, 시그모이드 함수를 미분하였을 때 다음 식으로 바꿀 수 있습니다.
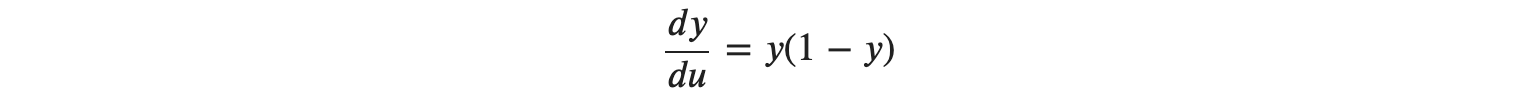
그다음,𝑑𝑢𝑑𝑥 즉 𝑢를 𝑥에 관해 미분하면 𝑑𝑢𝑑𝑥=𝑤 이므로 최종적인 결과는 다음처럼 계산이 가능합니다.
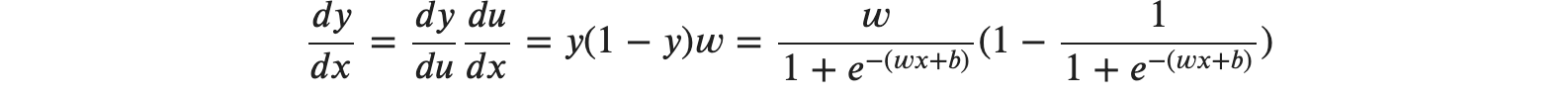
다변수 함수의 연쇄법칙
변수가 여러 개인 다변수 함수에도 연쇄법칙을 적용할 수가 있습니다. 위처럼 분수를 다루듯이 미분 방정식을 변형하겠지만 관련된 모든 변수에 연쇄법칙을 적용할 필요가 있으므로 단순하지는 않습니다.
먼저 변수가 2개인 함수일 때를 생각해 보도록 하겠습니다. 𝑧=𝑓(𝑢,𝑣)라는 함수가 있고, 𝑢와 𝑣 역시 각각 𝑢=𝑔(𝑥,𝑦)와 𝑣=ℎ(𝑥,𝑦)라는 함수라는 함수라고 생각할 때, 𝑧=𝑓(𝑔(𝑥,𝑦),ℎ(𝑥,𝑦))라고 바꿀 수 있습니다. 이때 다음과 같은 다변수 함수의 연쇄법칙이 성립하게 됩니다.

x에 대한 편미분을 구해서 x가 포함된 모든 함수에 대한 미분값에 연쇄법칙을 적용시킨 다음 더해주면 됩니다. 다변수 함수의 예를 한번 들어보겠습니다.
이변수 함수가 𝐶=𝑢2+𝑣2이고, 𝑢=𝑎𝑥+𝑏𝑦, 𝑣=𝑝𝑥+𝑞𝑦 (𝑎,𝑏,𝑝,𝑞 는 상수)라면 연쇄법칙의 계산 과정은 다음과 같습니다.

오늘은 간단하게 미분의 연쇄법칙에 대하여 알아보았습니다.
다음 세션으로는 수식을 통한 오차역전파법을 이해해 보도록 하겠습니다.
'Programming > Deep Learning' 카테고리의 다른 글
| [Python/DeepLearning] #10.3. 역전파) 계산 그래프를 통한 역전파 이해 (1) | 2024.02.15 |
|---|---|
| [Python/DeepLearning] #10.2. 역전파) 수식을 통한 오차역전파법 이해 (0) | 2024.02.08 |
| [Python/DeepLearning] #9.3. MNIST 신경망 구현하기 (2) | 2024.02.02 |
| [Python/DeepLearning] #9.2. 수치 미분과 경사하강법(하) (1) | 2024.01.31 |
| [Python/DeepLearning] #9.1. 수치 미분과 경사하강법(상) (0) | 2024.01.29 |