지난 블로그에서는 합성함수의 미분과 연쇄법칙에 대하여 알아보았습니다.
이번에는 수식을 통한 오차역전파법에 대하여 알아보도록 하겠습니다!
오차역전파법
가중치 매개변수에 대한 손실 함수의 기울기를 구하기 위해 이전에 경사하강법을 수치 미분을 이용해 구현해 보았습니다. 수치 미분은 단순하고 구현하기도 쉽지만 계산 시간이 오래 걸린다는 치명적인 단점이 있습니다. 이번에 배워볼 오차역전파법(Back Propagation)은 가중치 매개변수의 기울기를 효율적으로 계산시킬 수 있습니다.
비용함수(Cost Function) 미분의 어려움
최적의 가중치와 편향을 구할 수 있는 지표로써 비용함수(Cost Function)를 사용한다고 앞서 배웠습니다. 경사하강법을 이용하지 않고 가중치와 편향을 구해 볼 수도 있는데, 어떻게 해결하고, 왜 경사하강법을 사용해야 하는지 먼저 살펴보겠습니다. 이미지 입력을 예로 들어볼 텐데요, 3 X 4 형태의 이미지를 64개 입력한다고 생각해 보겠습니다.
- 입력층엔 12개의 데이터 (𝑥1 ~ 𝑥12)
- 은닉층에 3개의 유닛
- 출력층에 2개의 유닛
위의 규칙에서 비용함수로 제곱오차식을 이용한다고 생각하고, 64개의 이미지를 입력한다라고 예상 해 봤을 때 𝑘번째 이미지의 제곱오차값 𝐶를 𝐶𝑘로 두면 다음과 같은 식을 구할 수 있습니다.
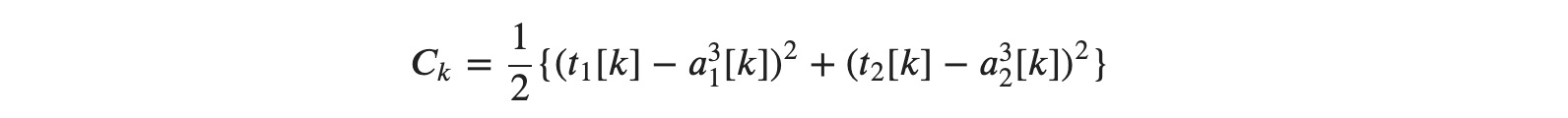
위의 식에서 𝑡는 𝑘 번째 이미지의 정답 데이터, 𝑎는 신경망이 예측한 데이터입니다. 이를 학습 데이터 전체로 적용한다고 생각하면
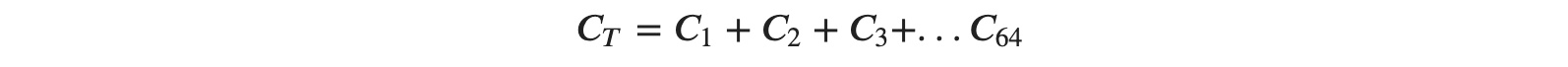
라는 비용함수 𝐶𝑇를 얻을 수 있습니다. 하지만 비용함수 𝐶𝑇는 매우 복잡한 함수입니다. 결정해야 할 가중치와 편향은 47개나 있습니다. (입력값 12개 X 입력에 대한 유닛의 가중치 3개 + 각 유닛별 편향 3개) + ( 출력층으로 향하는 입력값 3개 X 출력층으로 향하는 가중치 2개 + 출력층의 편향 2개)
따라서 각 가중치와 편향을 결정하기 위한 미분 방정식 자체가 총 47개라는 이야기가 됩니다.
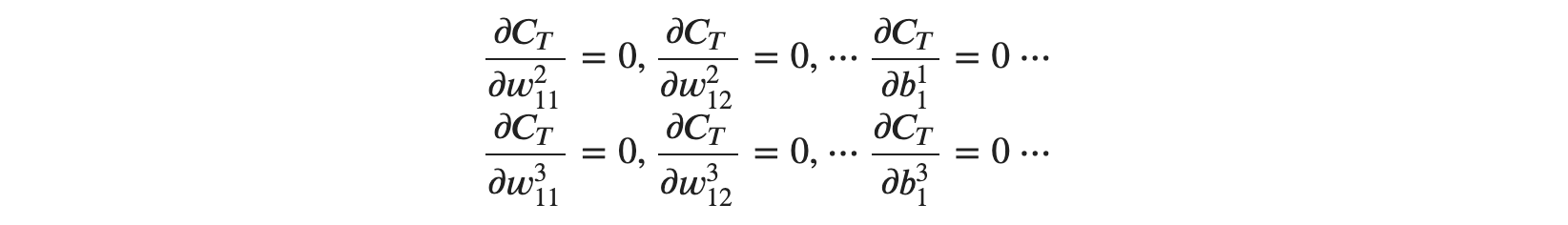
위의 방정식을 푸는 것은 매우 어렵기 때문에 경사하강법이 등장합니다.
다시 살펴보는 경사하강법
다시 경사하강법을 정리해 보기 전 수학적으로 경사하강법을 정리해 보도록 하죠
미분 가능한 함수 𝑓(𝑥1,𝑥2,⋯,𝑥𝑛))에서 변수에 차례로 𝑥1+Δ𝑥1,𝑥2+Δ𝑥2,⋯,𝑥𝑛+Δ𝑥𝑛 이라고 작은 값을 더해 변화시켰을 때 함수 𝑓가 최솟값이려면 다음 함수가 성립합니다.
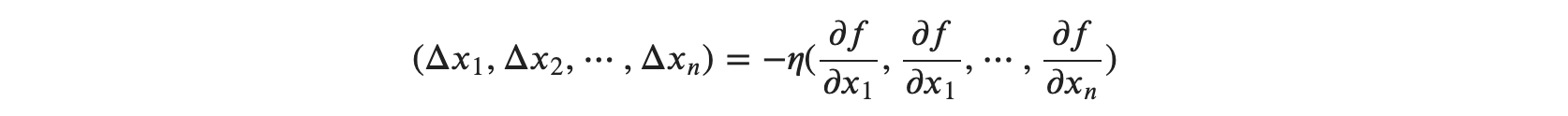
위 식을 가중치와 편향을 갖는 식에 대입해 봤을 때는 다음과 같이 정리가 가능합니다.
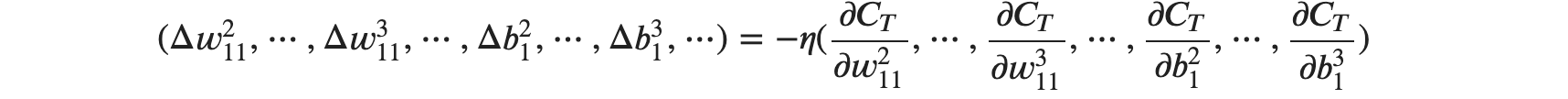
위의 식을 이용하면 컴퓨터에서 𝐶𝑇가 최솟값이 되는 가중치 및 편향을 계산할 수 있습니다. 좌변에 위치한 현재 매개변수의 위치에 우변에서 구현 변위 벡터를 더하면 새로운 위치가 구해진다고 볼 수 있는데요, 이를 매개변수들에 대한 행렬로 만들어 일반화시키면 다음과 같습니다.
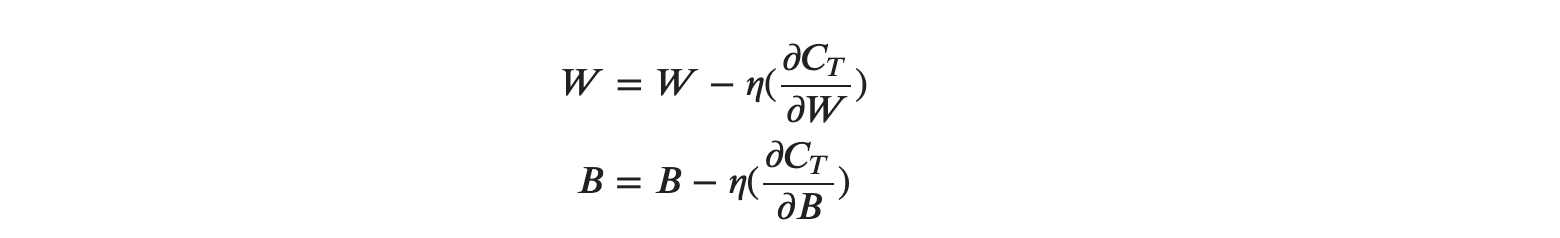
위 계산식을 반복하여 최솟값이 되는 가중치와 편향을 계산한다고 보면 될 것 같습니다.
미분지옥
다시 한번 경사하강법이 아닌, 일반적인 다변수 미분을 통해 살펴볼 것이 있습니다. 위의 예에서 47개의 파라미터가 존재하고, 이를 미분을 통해 구해야 한다고 이야기했는데요, 간단한 예로 성분 𝑤211의 기울기를 계산해 보겠습니다.
𝑘 번째 이미지에서 얻은 출력과 정답 데이터의 제곱오차식 𝐶𝑘에 대한 𝑤211의 기울기는 다음과 같이 구할 수 있습니다.
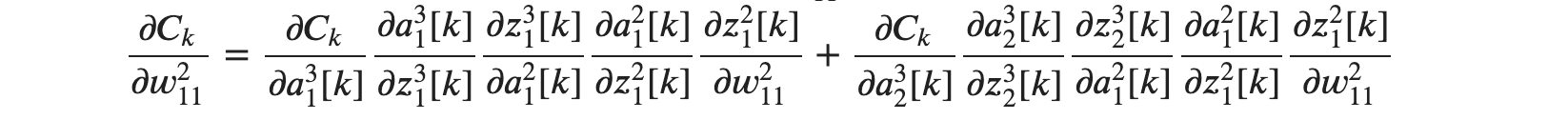
입력데이터를 넣었을 때 처음으로 만날 수 있는 가중치인 𝑤211을 구하는데도 어마어마한 식이 필요한 것 같습니다. 여기서 64번째 이미지까지의 𝑤211의 기울기를 구해보면 식은 다음과 같이 정리가 가능합니다.

위 식의 각 항마다 = 0을 붙여서 미분방정식으로 만들어 계산하면 편미분 결과를 가중치와 편향의 식으로 표현이 가능하겠죠?
항 하나하나의 계산은 단순하지만 여러 항을 한꺼번에 계산하려면 '미분 지옥'이라고 하는 미분의 복잡성과 방대함에 압도당하고 맙니다. 그래서 고안된 것이 오차역전파법(Back Propagation)입니다.
기울기 계산에 대한 단순화
상당히 복잡한 위 계산 과정에서 발견할 수 있는 특징이 있는데, 바로 기울기 성분은 학습 결과 하나하나의 단순한 합이라는 것입니다. 즉, 비용함수 𝐶𝑇의 편미분은 유닛마다 얻어낸 학습 결과 각각에서 얻은 미분의 합이라고 볼 수 있습니다! 즉, 가중치에 대한 기울기를 구하려면 제곱오차 𝐶의 편미분을 구한 결과에 학습 데이터를 대입한 후 학습 결과 전체를 더하면 64번의 편미분을 계산한 결과를 얻어낼 수 있다는 이야기입니다. 즉! 복잡해 보이는 위 수식에서 𝑎,𝑧 는 모두 우리가 구할 수 있는 상숫값 이라는 것입니다.
즉 𝐶𝑇의 편미분의 결과에 학습 데이터만 입력하면 실제 우리가 할 계산은 아래와 같이만 하면 된다는 이야기가 됩니다!
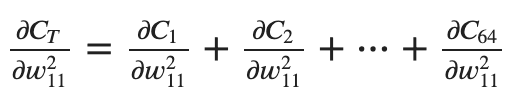
유닛의 오차(𝛿𝑙𝑗)
간단한 다변수 함수의 최솟값을 찾을 때는 제일 단순하고 쉽게 구할 수 있는 경사하강법이 효율적이지만, 변수와 파라미터가 함수와 복잡하게 얽혀 잇는 신경망이라면 경사하강법조차 계산하기 어려워져 그대로 사용할 수가 없게 됩니다. 미분 지옥에 빠져버린다는 뜻이죠, 그래서 등장한 것이 오차역전파법입니다.
오차역전파법은 복잡한 미분의 계산을 '수열의 점화식'으로 대체합니다. 이 점화식을 제공할 수 있는 것이 각 유닛의 오차(error)라고 불리는 변수 𝛿𝑙𝑗입니다. 제곱 오차 𝐶를 이용하여 정의하면 다음과 같습니다.
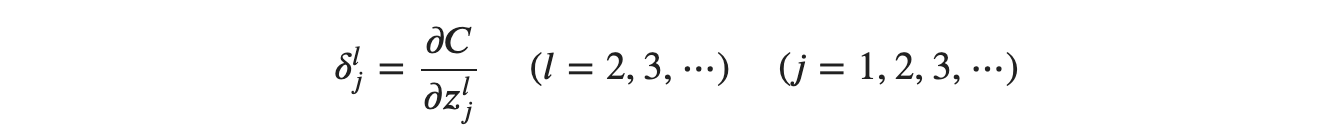
위의 식에서 𝑙은 레이어의 인덱스, 𝑗는 유닛의 인덱스를 의미합니다. 만약 2층 1번째 유닛의 오차와 3층 2번째 유닛의 오차를 구한다면 다음과 같이 구할 수 있겠습니다.
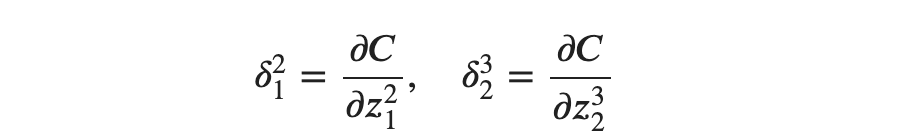
𝑧는 일단 입력값, 가중치와 편향을 통해 얻어진 값이라고 판단할 수 있습니다. 하지만 우리가 원하는 것은 언제나 비용함수(손실함수)의 값을 최소화할 수 있는 𝑤를 원하기 때문에, 손실함수 𝐶에 대한 𝑤를 계산하기 위해 다음과 같이 먼저 생각해야 합니다. 즉 ∂𝐶∂𝑤를𝛿𝑙𝑗로 표현하기 위한 과정을 지금부터 알아보겠습니다.
먼저 편미분의 연쇄법칙을 이용해 ∂𝐶∂𝑤211211를 알아보겠습니다.
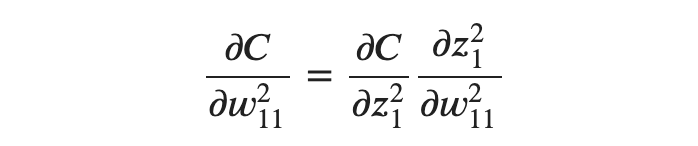
여기서 𝑧2121은𝑧21=𝑤211𝑥1+𝑤212𝑥2+⋯+𝑏21이기 때문에 다음 식을 도출해 낼 수 있습니다.

위의 식을 모두 정리해 보면 다음과 같은 수식이 완성됩니다.
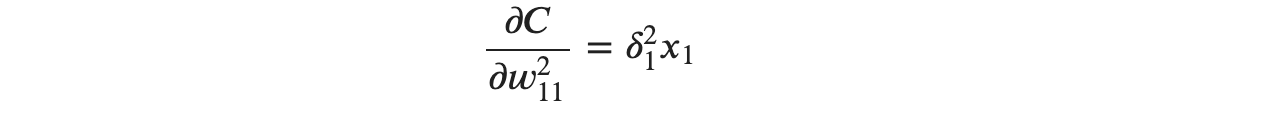
이것은 무엇을 의미할까요? 손실함수에 대한 가중치의 변화량을 구하기 위해서는, 현재 층의 오차에다가 이전 층에서 흘러들어오고 있는 우리가 알 수 있는 값을 곱했다는 것을 알 수 있습니다! 조금씩 오차역전파법에 다가서고 있습니다. 아직 끝이 아닙니다. 위의 식을 일반화 해보기 위해서 다른 유닛에 대한 내용도 알아보겠습니다. 이번엔 ∂𝐶∂𝑤311 (출력층)을 𝛿𝑖𝑗로 표현해 보겠습니다.
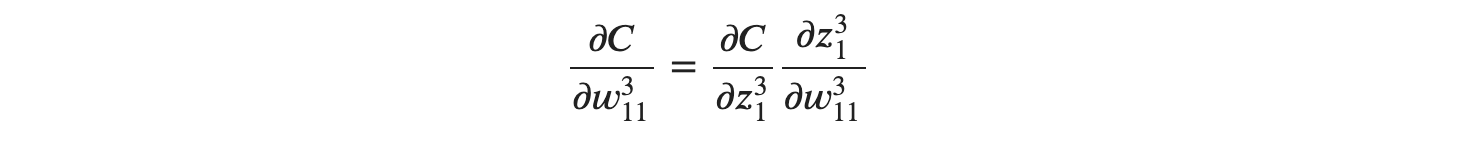
위의 식에서는 입력값인 𝑥1,𝑥2 같은 형태로 표현했지만, 유닛을 지나온 값이기 때문에 활성화 함수가 적용되어 𝑎1,𝑎2로 표현하면 𝑧31은 다음과 같이 표현 가능합니다.
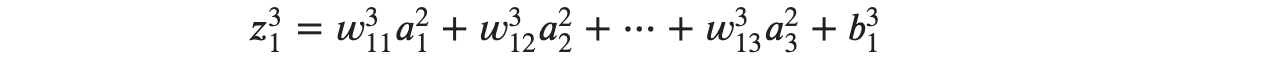
아까와 비슷하게 ∂𝑧31∂𝑤311을 구해보면 그 결과는 𝑎21가 등장합니다. 최종적으로
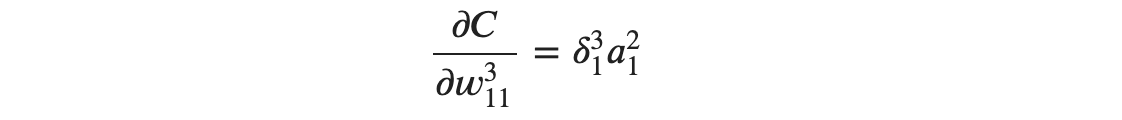
로 정리가 가능합니다. 그렇다면 편향 𝑏는 어떨까요? 계산 과정은 똑같습니다. 그 결과 𝑏21,𝑏31의 편미분은 다음과 같아집니다.
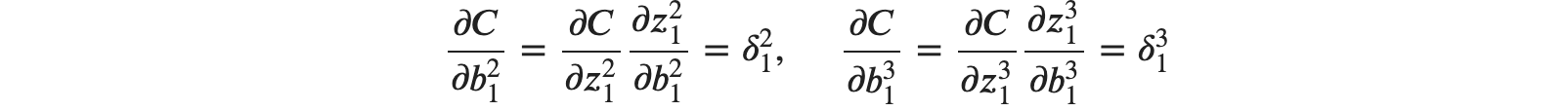
편향 𝑏는 그 오차가 그대로 편미분 값으로 적용된다고 볼 수 있네요. 그렇다면 마지막으로 𝛿𝑙𝑗을 일반화 해보면 다음과 같이 정리가 됩니다.
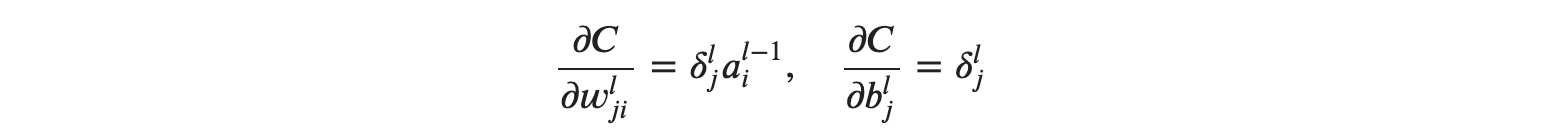
위의 정리된 식에서 𝑙은 현재 층 인덱스, 𝑗는 다음 유닛의 인덱스, 𝑖는 이전 유닛의 인덱스를 의미합니다. 여기서 추가적으로 살펴봐야 할 사실은 𝛿𝑙𝑗와 𝛿𝑙+1𝑗의 관계에 대해서 알아볼 필요가 있습니다.
위의 일반화된 식의 의미는 유닛의 오차 𝛿𝑙𝑗만을 구하게 되면 경사하강법을 위한 비용함수 𝐶의 편미분도 한꺼번에 구할 수 있다는 이야기가 됩니다. 정리해 보겠습니다.

이어서 알아볼 내용은 무엇일까요? 신경망에서의 𝛿𝑙𝑗과 𝛿𝑙+1𝑗의 관계에서 𝛿𝑙𝑗을 구하는 오차역전파법을 실제로 다뤄 보는 것입니다!
신경망과 오차역전파법
오차역전파법은 유닛의 오차 𝛿𝑙𝑗의 점화식을 먼저 만들고, 해당 점화식에서 복잡한 미분 계산을 해결하는 방법입니다. 오차역전파법은 복잡한 미분 계산을 단순히 수열의 점화식으로 만들어 버린다는 점입니다. 이제 실제 신경망에서 오차역전파법을 적용시키는 방법에 대해 이야기해 보겠습니다.
오차역전파법은 𝑙층 𝑗번째 유닛이라고 할 수 있는 변수 𝛿𝑙𝑗을 정의합니다. 그리고 𝛿𝑙𝑗을 이용하면 제곱오차(손실함수)에 대한 기울기도 구할 수 있었는데요, 𝛿𝑙𝑗을 단순한 수열에 비유하면 정말 쉽게 말항(마지막 항)을 구해낼 수 있습니다.
수열 {𝛿𝑙𝑗}의 말항에 해당하는 오차, 즉 출력층의 오차를 구한다고 했을 때 세울 수 있는 식은 𝛿3𝑗(𝑗=1,2) 으로 설정하고 오차를 구해보도록 하겠습니다.
활성화 함수는 ℎ(𝑧)로 정의해 보도록 하겠습니다.
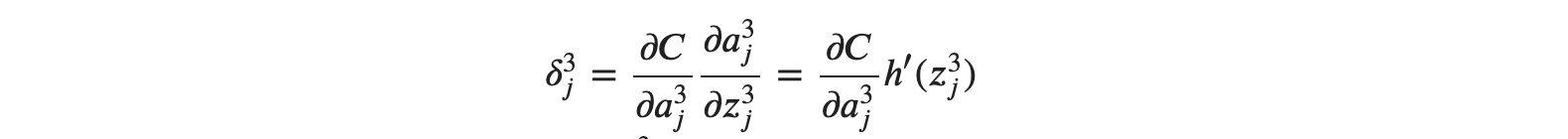
위 식에서 제곱오차 𝐶 및 활성화 함수에 대한 미분값 ℎ′(𝑧3𝑗)이 주어졌습니다. 이를 이용하면 손쉽게 말할에 해당하는 출력층 유닛의 오차도 구할 수 있습니다.
출력층의 층 번호를 𝐿로 일반화 해서 표현이 가능합니다.
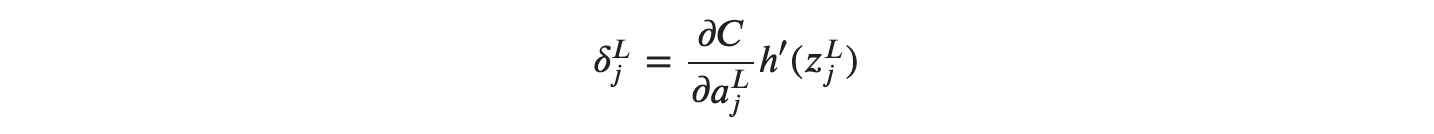
그렇다면 신경망 유닛의 오차 𝛿31을 구해보겠습니다. 활성화 함수 ℎ(𝑧)는 시그모이드 함수𝜎(𝑧)로 하겠습니다. 제일 먼저 해야 할 일은 제곱오차 𝐶를 𝑎3131로 편미분 하는 것부터 시작합니다.
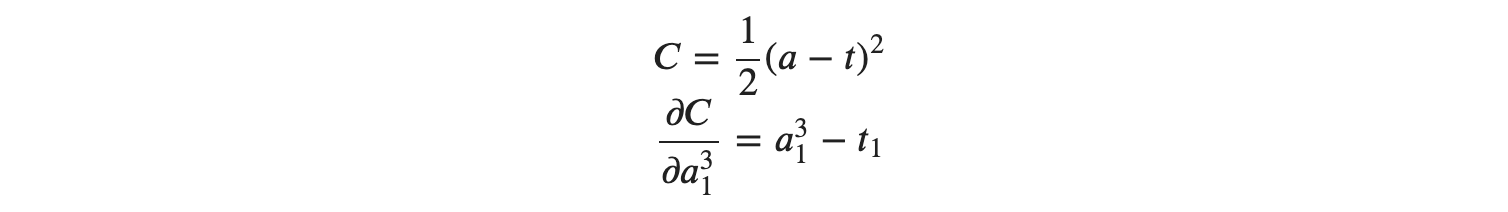
위 식을 유닛의 오차를 구하기 위한 식에 대입하면 다음과 같습니다.
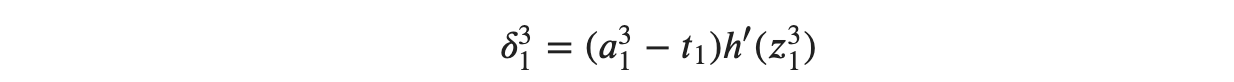
𝛿32 역시 같은 방식으로 계산이 가능합니다.
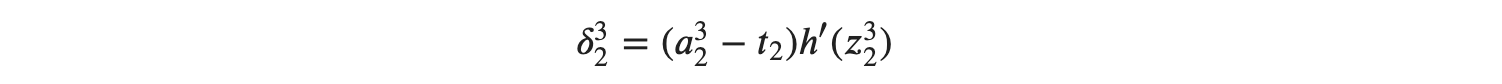
여기서 시그모이드 함수를 미분했었던 공식을 적용시키면
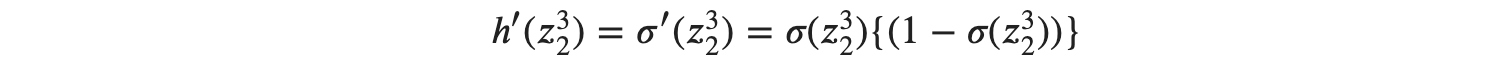
으로 ℎ′(𝑧32)를 구체화시킬 수 있게 되고, 이를 최종적으로 적용시키면
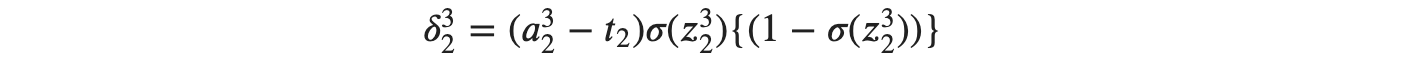
식이 유도 됩니다. 위에서 유도된 식은 출력층에 대한 식입니다. 그렇다면 이전 층인 은닉층에 대한 𝛿𝑙𝑗은 𝛿𝑙+1𝑗과 간단한 관계식으로 연결되어 있기 때문에 𝛿𝑙+1𝑗을 이용해 𝛿𝑙𝑗을 구하는 것도 가능해집니다. 편미분의 연쇄 법칙을 이용해서 𝛿21에 대한 다음 식을 유도할 수 있습니다.
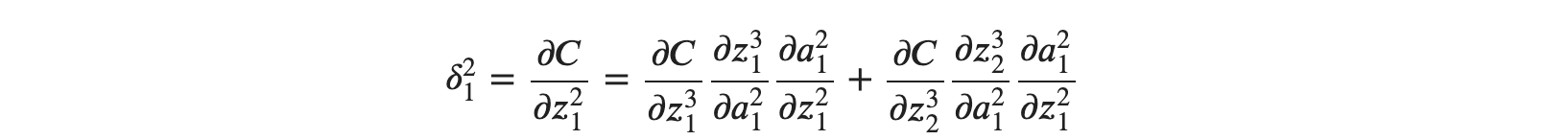
잘 살펴보면 출력층으로부터 제곱오차를 편미분 하여 이전에 흘러들어온 값(𝑎)에 대한 𝑧의 편미분 값을 연쇄법칙으로 구하고 있는 모습이 보입니다. 위를 부분별로 살펴보도록 하겠습니다. 먼저 ∂𝐶∂𝑧31과∂𝐶∂𝑧32은 𝛿 형태로 나타낼 수 있을 것 같습니다.
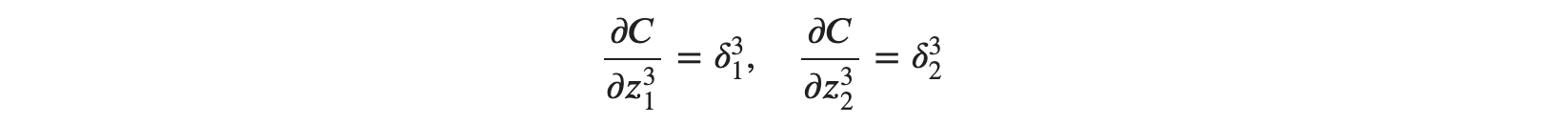
그다음∂𝑧31∂𝑎21와 ∂𝑧32∂𝑎21은 각각 다음처럼 구할 수 있습니다.
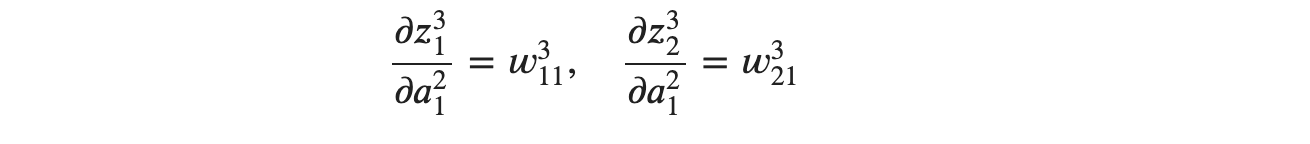
마지막 ∂𝑎21∂𝑧21는 활성화 함수 ℎ(𝑧)를 통해 다음처럼 구할 수 있습니다.
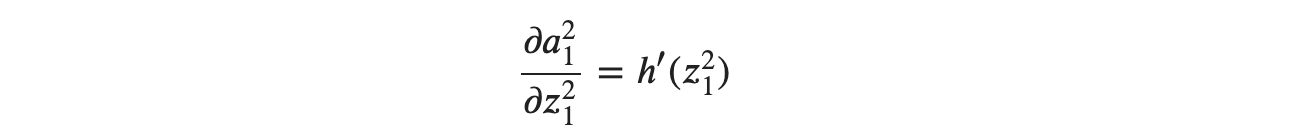
이제 마지막으로 정리를 해보면
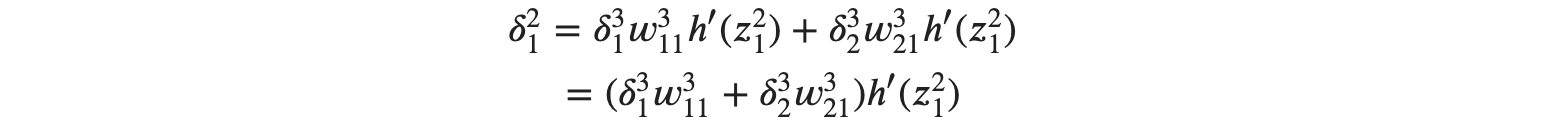
으로 𝛿21을 나타낼 수 있습니다. 𝛿22 와 𝛿23도 똑같이 정리할 수 있습니다.
이제 2층과 3층의 관계를 일반화시켜 볼 수도 있을 것 같습니다.
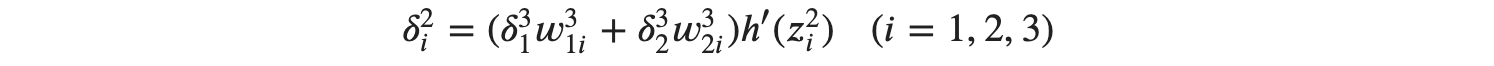
로 확인 2층과 3층의 관계에 대해 이야기할 수 있습니다. 이는 다시 𝑙층과 그다음 층인 𝑙+1의 관계식으로 일반화할 수 있습니다.
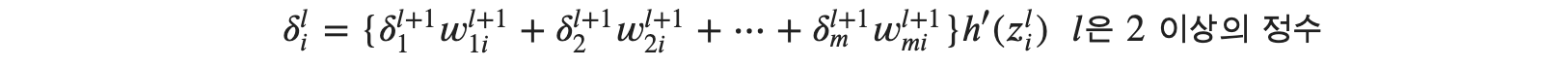
미분을 하지 않았다?
수식 (𝛿31𝑤31𝑖+𝛿32𝑤32𝑖)ℎ′(𝑧2𝑖)을 살펴보면 𝛿31과 𝛿32은 각각 𝛿31=(𝑎31−𝑡1)ℎ′(𝑧31)과 𝛿32=(𝑎32−𝑡2)ℎ′(𝑧32)에서 얻을 수 있는 것이 확인됩니다. 즉 수식 (𝛿31𝑤31𝑖+𝛿32𝑤32𝑖)ℎ′(𝑧2𝑖)을 이용하면 층 2의 𝛿2𝑖의 값을 미분하지 않고 구할 수 있다는 뜻이 됩니다.
이것이 바로 오차역전파법입니다! 출력층에 있는 유닛의 오차만 구하면, 다른 유닛의 오차는 편미분 할 필요가 없게 됩니다. 보통 층의 번호가 높은 방향에서 층의 번호가 낮은 방향으로 값을 정해나갑니다. 이는 순차대로 흘러가는 수열과 반대되기 때문에 역이라는 단어를 사용하게 되는 것입니다. 마지막으로 실제 계산 예를 확인해 보겠습니다. 𝛿22를 구한다고 가정하고, 활성화 함수는 시그모이드 함수𝜎(𝑧)를 사용해 보겠습니다.
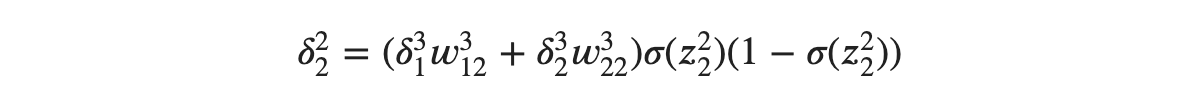
위 과정에서 확인할 수 있듯이, 미분 없이 𝛿22를 구하였습니다.
넘나 어렵죠... 수식을 통해서 오차역전파법을 이해하는 것이 좋지만, 다음은 조금 더 쉽게 이해할 수 있는 그림을 통한 오차역전파법을 다시 알아보겠습니다!
'Programming > Deep Learning' 카테고리의 다른 글
| [Python/DeepLearning] #10.4. 역전파) 덧셈 노드와 곱셈 노드 (0) | 2024.02.22 |
|---|---|
| [Python/DeepLearning] #10.3. 역전파) 계산 그래프를 통한 역전파 이해 (1) | 2024.02.15 |
| [Python/DeepLearning] #10.1. 역전파) 합성함수의 미분과 연쇄법칙 (1) | 2024.02.06 |
| [Python/DeepLearning] #9.3. MNIST 신경망 구현하기 (2) | 2024.02.02 |
| [Python/DeepLearning] #9.2. 수치 미분과 경사하강법(하) (1) | 2024.01.31 |