앞서 퍼셉트론에 대하여 알아보며, 단층 & 다층 퍼셉트론에 대한 이야기를 나눠 보았습니다.
2023.08.16 - [Programming/Deep Learning] - [Python/DeepLearning] #2. 퍼셉트론 (단층 & )
[Python/DeepLearning] #2. 퍼셉트론 (단층 & 다층)
이번 블로그에서는 퍼셉트론에 대하여 알아보도록 하겠습니다. 퍼셉트론의 개념은 1957년도에 구현된 알고리즘이며, 신경망(딥러닝)의 기원이 되는 알고리즘이라고 할 수 있습니다. 즉, 퍼셉트
yuja-k.tistory.com
다층 퍼셉트론은 단층 퍼셉트론만으로는 계산할 수 없는 복잡한 함수들을 표현할 수 있다는 사실을 알게 되었습니다.
신경망의 등장
이 처럼 여러 개의 다층 퍼셉트론을 층처럼 겹겹이 쌓은 것을 인공 신경망 (Neural Network)라고 합니다.
활성화 함수( activation function)
인공 신경망의 퍼셉트론을 유닛 혹은 노드라고 불립니다. 각 유닛은 입력 값을 받아 해당 입력 값의 가중치를 이용해 계산을 한다는 것을 퍼셉트론을 공부하며 알았습니다. 다시 한번 퍼셉트론에서 보았던 입력 값이 두 개일 때의 수식을 확인해 보겠습니다!
퍼셉트론을 공부하며 확인했던 𝑦가 활성화( 1로 출력 ) 되는 조건 수식은 완벽한 계단 함수(u)였었습니다.
위 계단 함수식이 바로 각 유닛의 출력값을 0 또는 1로 설정하기 위한 퍼셉트론( 유닛 또는 노드 )의 활성화 함수가 됩니다. 즉 계단 함수를 이용해 퍼셉트론의 결과물을 0 또는 1로 활성화시키는 조건을 마련했다고 생각하면 됩니다. 계단 함수만을 사용하지 않고, 다른 활성화 함수들에 대해 공부해 볼 텐데요, 이때 𝑦가 출력 되기 위한 활성화 함수를 적용시킨 수식은 다음과 같이 일반화시켜 볼 수 있겠습니다.
위의 𝑎를 활성화 함수라고 이야기하며, 각 입력값에 대한 활성화 함수를 적용시켜 최종적으로 𝑦값이 결정된다고 보면 됩니다. 중요한 점은 생물학적이라는 조건을 굳이 주지 않으면 0과 1로 표현하지 않아도 된다라는 점입니다. 하지만 우리가 지금까지 봐왔던 활성화 함수인 𝑢(𝑧)는 0과 1로만 표현하기 때문에, 신경망에서 자주 사용되는 다른 활성화 함수들에 대해 이야기해 볼까 합니다. 사실 퍼셉트론에서는 활성화 함수로 계단 함수를 이용한다라고 이야기합니다. 즉, 활성화 함수로 쓸 수 있는 여러 후보 함수 중에 퍼셉트론은 계단 함수를 채용하고 있다고 생각하면 됩니다. 이는 퍼셉트론, 즉 유닛(노드)의 활성화 함수를 우리 마음대로 바꿀 수 있다고 생각하는 것이 우리가 배울 딥러닝 인공 신경망의 시작이라고 생각해 볼 수 있을 것입니다.
비선형 함수
앞서 이야기해 본 계단 함수, 그리고 뒤에 이야기할 시그모이드(𝜎(𝑧))와 ReLU 함수 모두 비선형 함수입니다. 신경망에서는 활성화 함수로 비선형 함수를 사용해야 합니다. 왜냐하면 선형 함수를 사용하게 되면 신경망의 층을 깊게 해서 네트워크를 구성하는 것이 의미가 없어지기 때문입니다.
예를 들어 활성화 함수로𝑎(𝑥)=𝑐𝑥를 사용한다고 했을 때 3층 네트워크를 구축하게 되면
𝑦(𝑥)=ℎ(ℎ(ℎ(𝑥)))
가 됩니다. 즉,
𝑦(𝑥)=𝑐∗𝑐∗𝑐∗𝑥
처럼 곱셈을 세 번 수행하는 것처럼 보이지만 실제로는
𝑦(𝑥)=𝑎𝑥
와 똑같은 식이 되어 버립니다. 그냥𝑎=𝑐33이라고 생각해 버리면 끝이기 때문이죠. 이는 은닉층을 여러 층으로 구성하는 이점을 살릴 수가 없기 때문에 비선형 함수를 이용해서 은닉층들을 구성합니다.
No.1 "시그모이드 (𝜎)"
시그모이드 함수(sigmoid function) 𝜎(𝑧)는 가장 유명한 활성화 함수의 예시입니다. 수식 𝑧은 다음과 같습니다.
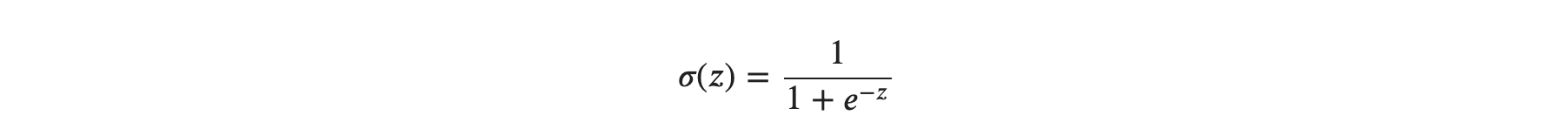
시그모이드 함수 𝑢(𝑧)의 출력은 항상 0보다 크고 1보다 작은 임의의 실숫값이 됩니다. 또한 미분 가능 함수라고 볼 수 있는데요. 이 두 가지 특징이 시그모이드 함수를 사용하는 이유가 됩니다. 계단 함수와 시그모이드 함수를 시각적으로 확인해 보겠습니다.
import numpy as np
import matplotlib.pyplot as plt# 계단 함수 구현
def step_function(x):
return np.array( x > 0, dtype=np.int )
# 시그모이드 구현
# np.exp 함수를 이용해 자연상수(e) 의 지수함수를 구현 할 수 있다.
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 시각화
fig, (ax1, ax2) = plt.subplots(1, 2,figsize=(20,8))
x = np.arange(-5.0, 5.0, 0.1)
ax1.plot(x, step_function(x))
ax1.set_title('step function')
ax2.plot(x, sigmoid(x))
ax2.set_title('sigmoid function')
plt.show()
계단 함수의 출력값은 반응 여부를 표현하는 0 또는 1입니다. 하지만 시그모이드 함수는 언제나 0보다 크고 1보다 작은 값을 출력하며, 이는 각 유닛의 흥분도 또는 반응도를 나타냅니다. 시그모이드 함수는 계산식 𝑧의 결과물이 몇이 나오던 항상 0 또는 1에 가까운 값이 되게 됩니다. 이는 각 유닛의 '흥분도' 또는 '반응도'를 나타내게 되며, 이는 출력값이 1에 가까우면 흥분도가 높고, 0에 가까우면 흥분도가 낮다고 생각할 수 있게 됩니다. 참고로 이 흥분도를 둔감하게, 또는 민감하게 만들어 주는 것이 편향 ( bias )입니다.
시그모이드 함수와 계단 함수의 비교
위의 계단함수와 sigmoid 함수를 비교해 보겠습니다. 공통점과 차이점을 알아볼 텐데요.
제일 먼저 느껴지는 차이는 매끄러움입니다. 시그모이드 함수는 부드러운 곡선의 형태를 띠고 있으며 입력에 따른 출력이 연속적으로 변화되는 것이 확인됩니다.
그에 반에 계단 함수는 어느 순간 계단 형태로 출력이 갑작스레 변화되는데요, 시그모이드의 매끄러움이 신경망 학습에서 중요한 역할을 하게 됩니다. 계단 함수는 0과 1중 하나의 값만 돌려주는 반면에, 시그모이드 함수는 실수 형태로 돌려줍니다. 즉, 퍼셉트론에서는 0과 1만 출력되지만, 신경망에서는 연속적인 실수가 흐른다고 볼 수 있겠습니다. 둘의 공통점은 입력이 커지면 1에 가까워지거나 1이 되며, 반대로 입력이 작아지게 되면 0에 가까워지거나 0이 된다는 사실입니다.
즉, 계단 함수와 시그모이드 함수 모두 입력이 중요하면(입력값이 크면) 1에 가까워지고, 반대로 입력이 중요하지 않으면 작은 값(0에 가까워지는) 값을 출력한 닦도 이해할 수 있습니다.
No.2 "ReLU"
시그모이드 함수는 신경망 분야에서 오래전부터 이용해 왔었던 함수입니다.
최근에는 ReLU(Rectified Linear Unit) 함수를 많이 이용하는 추세입니다. ReLU는 간단합니다. 입력값이 0을 넘으면 그 입력을 그대로 출력하고, 0 이하면 0을 출력하는 함수입니다.
def relu(x):
return np.maximum(0, x)
#visualisation
x = np.arange(-5.0, 5.0, 0.1)
plt.title('ReLU function')
plt.plot(x, relu(x))
plt.show()
수식으로 나타내면 다음과 같습니다.
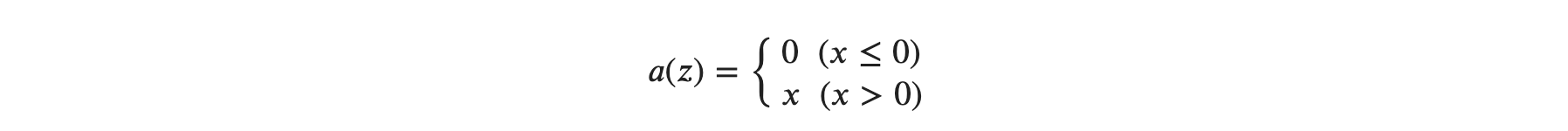
수식과 그래프에서 보는 것처럼 ReLU는 굉장히 간단한 함수입니다. 시그모이드 함수는 부드러운 곡선을 만들어서 신경망을 구축하고, ReLU는 여러 개의 직선을 연결해서 신경망을 구축합니다.
그런데 컴퓨터에서는 곡선을 만들어서 표현하는 것보다 직선을 여러 개 놓고 표현하는 것이 더 효율이 좋기 때문에 시그모이드보다 ReLU가 더 많이 사용되는 추세입니다.
다음 블로그에서는 다차원 배열의 계산에 대하여 알아보도록 하겠습니다!
'Programming > Deep Learning' 카테고리의 다른 글
| [Python/DeepLearning] #6. 출력층(output layer) 설계 (1) | 2023.10.11 |
|---|---|
| [Python/DeepLearning] #5. 행렬과 신경망 (0) | 2023.08.30 |
| [Python/DeepLearning] #4. 다차원 배열의 계산 (0) | 2023.08.23 |
| [Python/DeepLearning] #2. 퍼셉트론 (단층 & 다층) (0) | 2023.08.16 |
| [Python/DeepLearning] #1. Numpy 기초 총 정리 (0) | 2023.06.20 |