이번 포스팅은 다중 선형 분류에 대하여 알아보도록 하겠습니다
선형 이진 분류 또는 선형 회귀에 대해 알고 싶은 분들은 이전 포스팅들을 참고해 주세요~!
2023.05.09 - [Programming/특성 공학] - [Machine Learning] 선형 이진 분류
[Machine Learning] 선형 이진 분류
지난 선형 회귀 포스팅에 이어 이번 포스팅에서는 선형 이진 분류에 대하여 알아보도록 하겠습니다. 2023.05.02 - [Programming/특성 공학] - [Machine Learning] 선형 회귀 [Machine Learning] 선형 회귀 이번 블로
yuja-k.tistory.com
2023.05.02 - [Programming/특성 공학] - [Machine Learning] 선형 회귀
[Machine Learning] 선형 회귀
이번 블로그는 선형 모델에 대하여 알아보도록 합시다. 선형 모델은 매우 오래전 개발된 모델입니다. 선형 모델은 입력 특성에 대한 선형 함수를 만들어 예측을 수행합니다. 먼저 회귀의 선형
yuja-k.tistory.com
다중 클래스 분류란?
로지스틱 회귀는 기본적으로 softmax 함수를 이용하여 다중 분류를 지원하나, 다른 많은 모델들은 태생적으로 이진 분류만을 지원합니다. 즉 다중 클래스(Multi-class)를 지원하지 않습니다.
이진 분류 알고리즘을 다중 클래스 알고리즘으로 확장하는 방법은 일대다(One vs Rest 또는 One vs All) 방법입니다. 일대다 방식은 각 클래스를 다른 모든 클래스와 구분하도록 이진 분류 모델을 학습시킵니다.
결국 클래스의 개수만큼 이진 분류 모델이 만들어지며, 예측할 때 이렇게 만들어진 모든 이진 분류기가 작동하여 가장 높은 점수를 내는 분류기의 클래스를 예측값으로 선택하게 됩니다.
지금까지 해왔던 것과 마찬가지로 다중 클래스 분류도 어쨌든 이진 분류를 기반으로 생각해야 하기 때문에 방정식 자체가 똑같습니다.
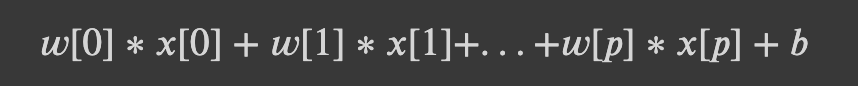
다중 클래스 로지스틱 회귀의 수학은 다른 모델들의 위의 일대다 방식과는 조금 다릅니다. 하지만 여기서도 클래스마다 계수 벡터와 절편을 만들며, 예측 방법도 같습니다.

𝑖번째 데이터 포인트 𝑋𝑖의 출력 𝑌𝑖가 클래스 𝑐일 확률 𝑃𝑟(𝑌𝑖=𝑐)는 𝐾개의 클래스에 대한 각각의 계수를 데이터 포인트에 곱하여 자연상수(𝑒)에 지수함수를 적용한 합으로써 클래스에 대한 값을 나누어 계산합니다.
위의 함수를 소프트맥스 함수 표현식이라 하며, 수식의 간소화를 위해 계수벡터에 절편 𝑏가 포함 되어 있는 것으로 나타냅니다.
따라서 다중 클래스 로지스틱 회귀에서도 계수 벡터와 절편이 존재합니다.
세 개의 클래스를 가진 간단한 데이터셋에 일대다 방식을 적용시켜 보겠습니다. 이 데이터셋은 2차원이며 각 클래스의 데이터는 정규분포(가우시안 분포)를 따릅니다.
#필요 라이브러리 임포트
from IPython.display import display
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import mglearn
from sklearn.model_selection import train_test_split
import platform
plt.rcParams['axes.unicode_minus'] = False
path = 'c:/Windows/Fonts/malgun.ttf'
from matplotlib import font_manager, rc
if platform.system() == 'Darwin':
rc('font', family='AppleGothic')
elif platform.system() == 'Windows':
font_name = font_manager.FontProperties(fname=path).get_name()
rc('font', family=font_name)
else:
print('Unknown system... sorry!')from sklearn.datasets import make_blobs
X, y = make_blobs(random_state=42)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
plt.legend(["클래스 0", "클래스 1", "클래스 2"])
이 데이터셋으로 먼저 LinearSVC 분류기를 훈련해 보겠습니다.
from sklearn.svm import LinearSVC
linear_svm = LinearSVC().fit(X, y)
print("계수 배열의 크기 : ", linear_svm.coef_.shape)
df_coef = pd.DataFrame(columns=["특성 0","특성 1"] ,data=linear_svm.coef_)
df_coef
print("절편 배열의 크기 : ", linear_svm.intercept_.shape)
df_intercept = pd.DataFrame(columns=["절편"], data = linear_svm.intercept_)
df_intercept
coef_ 배열의 크기는 (3,2)입니다. coef_의 행은 세 개의 클래스가 각각 대응하는 계수 벡터들을 각각 담고 있으며, 열은 각 특성에 따른 계수 값을 가지고 있습니다. intercept_는 각 클래스의 절편을 담아낸 1차원 벡터입니다.
세 개의 이진분류기가 만드는 경계를 시각화해보겠습니다.
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15) # -15 ~ 15 까지 50개의 수열을 생성
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_, mglearn.cm3.colors):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color) # 판별 함수 사용
plt.ylim(-10, 15)
plt.xlim(-10, 8)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
plt.legend(['클래스 0', '클래스 1', '클래스 2', '클래스 0 경계','클래스 1 경계', '클래스 2 경계'], loc=(1.01, 0.3))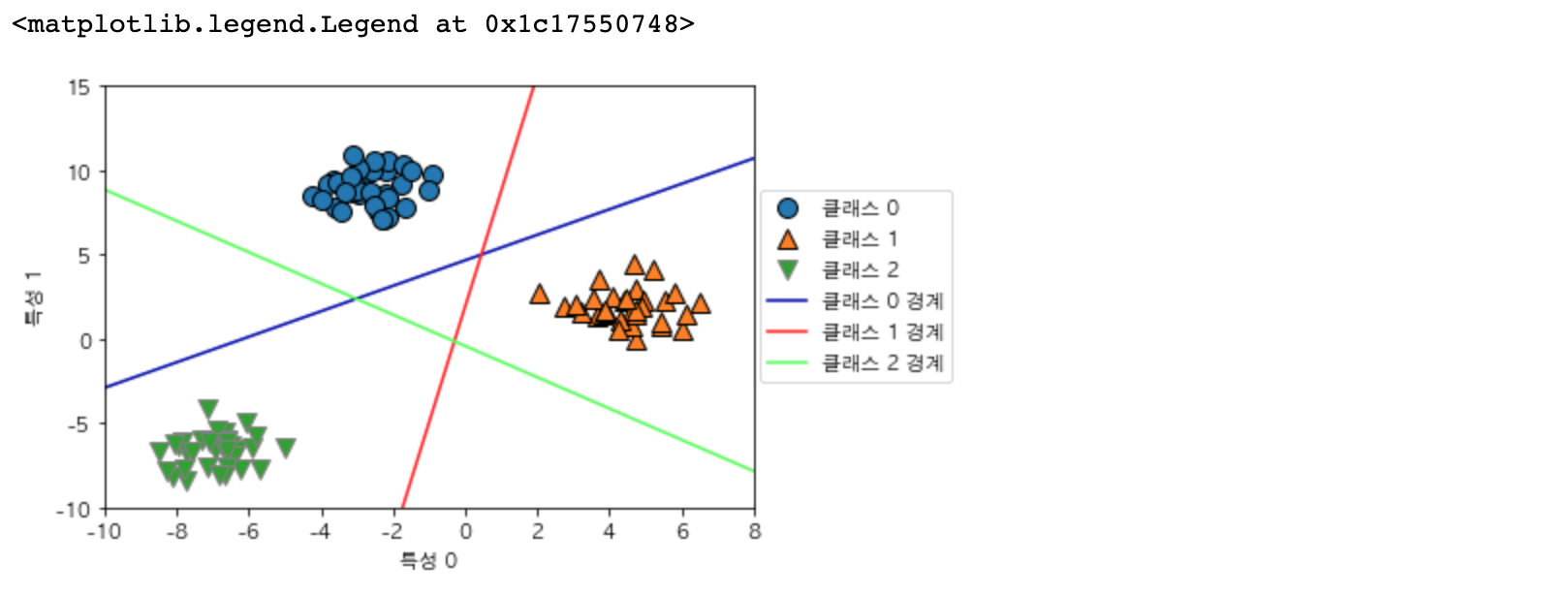
각 훈련 데이터의 클래스들에 대한 결정 경계를 그려 보았습니다. 파란색 선은 클래스 0으로, 주황색 선은 클래스 1로, 초록색 선은 클래스 2로 경계합니다. 각 경계에서 겹치는 부분들은 조금 더 가까운 쪽으로 예측을 하게 됩니다.
중앙의 삼각형 영역은 모든 데이터 포인트가 나머지로 분류한 곳으로써 분류 공식의 결과가 가장 높은 클래스가 포인트로써 지정되게 됩니다.
조금 더 알아보기 쉽도록 경계면을 그려 보겠습니다.
mglearn.plots.plot_2d_classification(linear_svm, X, fill=True, alpha=.7)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_, mglearn.cm3.colors):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.legend(['클래스 0', '클래스 1', '클래스 2', '클래스 0 경계', '클래스 1 경계', '클래스 2 경계'],
loc=(1.01, 0.3))
plt.xlabel('특성 0')
plt.ylabel('특성 1')
선형 모델의 주요 매개변수는 회귀 모델은 alpha, 분류 모델 (LinearSVC, LogisticRegression)에서는 C입니다. alpha의 값이 클수록, C 값이 작아질수록 모델은 단순해집니다.
회귀 모델은 이러한 매개변수를 조절하는 것이 꽤나 중요하며 보통 C와 alpha는 로그 스케일 ( 10배 단위로 조절 하는 것. 0.01, 0.1, 1, 10 등 )로 최적치를 정하게 됩니다.
또한 L1 규제와 L2 규제를 정해야 하는데 어떠한 규제를 사용해야 할지 결정 지어 주는 상황은 다음으로 정리해 볼 수 있겠습니다.
- 중요한 특성이 많지 않으면 L1 규제를 사용해 예측에 사용하지 않도록 만들 수 있습니다.
- 모델의 해석이 중요한 요소일 때도 ( 특정 요소가 매우 중요한 요소일 경우 ) L1 규제를 사용할 수 있습니다.
- 중요한 특성이 많으면 L2 규제를 사용해 약간이라도 예측에 영향을 미치도록 만들 수 있습니다.
선형 모델은 학습 속도가 빠르고 예측도 매우 빠릅니다. 매우 큰 데이터셋이던, 희소한 데이터셋이던 잘 작동합니다.
참고로 수십만 ~ 수백만 개의 샘플로 이뤄진 대용량 데이터 셋이라면 기본 설정보다 더 빨리 처리할 수 있도록 LogisticRegression과 Ridge에 solver='sag' 옵션을 부여해 줄 수 있습니다.
아니면 SGDClassifier 또는 SDGRegressor를 사용해 볼 수도 있습니다.
선형 모델은 샘플에 비해 특성이 많을 때 잘 작동하며 다른 모델로 학습하기 어려운 매우 큰 데이터셋에도 선형 모델을 많이 사용합니다.
하지만 저 차원의 데이터셋에서는 ( 특성이 많이 없는 ) 데이터셋에서는 다른 모델들의 일반화 성능이 더 좋습니다.
다음 블로그에서는 의사결정 트리에 대하여 다뤄보도록 하겠습니다!
'Programming > 특성 공학' 카테고리의 다른 글
| [Machine Learning] 의사결정 트리(Decision Tree) 시각화 (0) | 2023.05.30 |
|---|---|
| [Machine Learning] 의사결정 트리(Decision Tree) (0) | 2023.05.23 |
| [Machine Learning] 선형 이진 분류 (0) | 2023.05.09 |
| [Machine Learning] 선형 회귀 (0) | 2023.05.02 |
| [Machine Learning] 최근접 이웃(K-NN) (0) | 2023.04.24 |