지난 앙상블 모델에 이어 이번 블로그에서는 서포트 벡터 머신에 대하여 다루어 보도록 하겠습니다!
2023.06.06 - [Programming/특성 공학] - [Machine Learning] 앙상블 모델(Random Forest & Gradient Boosting)
[Machine Learning] 앙상블 모델(Random Forest & Gradient Boosting)
앞선 결정 트리의 개념에 더하여 이번 블로그에서는 앙상블 모델에 대하여 알아보도록 하겠습니다. 앙상블(ensemble)이란? 앙상블은 여러 머신러닝 모델을 연결하여 더 강력한 모델은 만드는 데에
yuja-k.tistory.com
이전에 분류용 선형 모델에서 잠시 LinearSVC를 잠깐 사용해 보았습니다.
2023.05.16 - [Programming/특성 공학] - [Machine Learning] 다중 선형 분류
[Machine Learning] 다중 선형 분류
이번 포스팅은 다중 선형 분류에 대하여 알아보도록 하겠습니다 선형 이진 분류 또는 선형 회귀에 대해 알고 싶은 분들은 이전 포스팅들을 참고해 주세요~! 2023.05.09 - [Programming/특성 공학] - [Machi
yuja-k.tistory.com
지금 해볼 SVM에 포함되는 모델인데요, SVM은 선형 모델과 다르게 단순히 선이나 평면으로 분류를 하지 않는 더 복잡한 모델을 만들 수 있도록 확장한 것입니다.
서포트 벡터 머신도 마찬가지로 분류, 회귀에 모두 사용할 수 있습니다.
다른 모델과 다르게 SVM은 수학적 의미가 너무나 복잡하기 때문에 다루지는 않겠습니다. 사용법과 원리에 대해서만 이야기해 보겠습니다.
선형 모델과 비선형 특성
직선과 초평면은 유연하지 못하다는 것을 우리는 선형 모델을 통해 이미 확인해 보았습니다. 즉 저 차원 데이터에서는 선형 모델이 매우 제한적이게 되는데요, 선형 모델을 유연하게 만드는 방법은 특성끼리 곱하거나 특성 자체를 거듭제곱하는 식으로 특성을 추가하는 것입니다.
#필요 라이브러리 임포트
from IPython.display import display
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import mglearn
from sklearn.model_selection import train_test_split
import platform
%matplotlib inline
plt.rcParams['axes.unicode_minus'] = False
path = 'c:/Windows/Fonts/malgun.ttf'
from matplotlib import font_manager, rc
if platform.system() == 'Darwin':
rc('font', family='AppleGothic')
elif platform.system() == 'Windows':
font_name = font_manager.FontProperties(fname=path).get_name()
rc('font', family=font_name)
else:
print('Unknown system... sorry!')from sklearn.datasets import make_blobs
X, y = make_blobs(centers=4, random_state=8)
y = y % 2
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
선형 모델은 직선으로만 데이터 포인트를 나누기 때문에 이러한 데이터셋에는 잘 들어맞지 않습니다.
from sklearn.svm import LinearSVC
linear_svm = LinearSVC().fit(X, y)
mglearn.plots.plot_2d_separator(linear_svm, X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
이번에는 특성 1의 제곱을 새로운 특성으로 추가해서 입력 특성을 확장해 보겠습니다. 즉 기존 특성 0, 특성 1만 있는 것이 아닌 [ 특성 0, 특성 1, 특성 1 제곱 ] 데이터가 추가됩니다.
X_new = np.hstack([X, X[:, 1:] ** 2])
from mpl_toolkits.mplot3d import Axes3D, axes3d
figure = plt.figure()
#3차원 그래프
ax = Axes3D(figure, elev=-152, azim=-26)
# y == 0인 포인트를 그리고 다음 y == 1 인 포인트를 그리기
mask = y == 0
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b', cmap=mglearn.cm2, s=60, edgecolor='k')
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^', cmap=mglearn.cm2, s=60, edgecolor='k')
ax.set_xlabel("특성 0")
ax.set_ylabel("특성 1")
ax.set_zlabel("특성 1 ** 2")
새로운 데이터셋에서는 선형 모델과 3차원 공간의 평면을 사용해 두 클래스를 구별할 수 있을 것 같습니다. 선형 모델을 만들어 확인해 보겠습니다.
linear_svm_3d = LinearSVC().fit(X_new, y)
coef, intercept = linear_svm_3d.coef_.ravel(), linear_svm_3d.intercept_
# 선형 결정 경계 그리기
figure = plt.figure()
ax = Axes3D(figure, elev=-152, azim=-26)
xx = np.linspace(X_new[:, 0].min() - 2, X_new[:, 0].max() + 2, 50)
yy = np.linspace(X_new[:, 1].min() - 2, X_new[:, 1].max() + 2, 50)
XX, YY = np.meshgrid(xx, yy)
ZZ = (coef[0] * XX + coef[1] * YY + intercept) / -coef[2]
ax.plot_surface(XX, YY, ZZ, rstride=8, cstride=8, alpha=0.3)
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b', cmap=mglearn.cm2, s=60, edgecolor='k')
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^', cmap=mglearn.cm2, s=60, edgecolor='k')
ax.set_xlabel("특성 0")
ax.set_ylabel("특성 1")
ax.set_zlabel("특성 1 ** 2")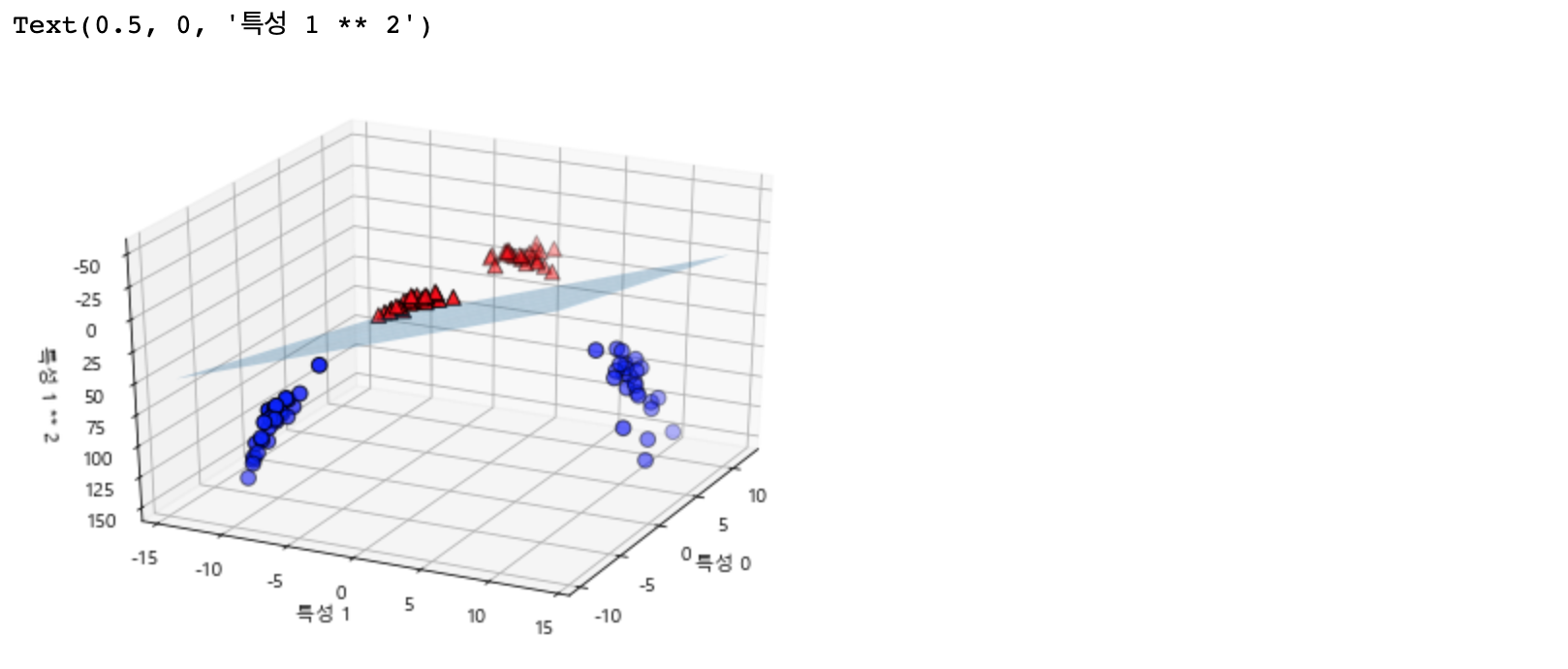
3차원으로 봐도 평면으로 결정 경계가 이루어지는 것을 볼 수 있습니다! SVM 모델을 사용하면 더 이상 선형이 아닌 직선 보다 타원에 가까운 비선형 모델을 만들어 냅니다.
ZZ = YY ** 2
dec = linear_svm_3d.decision_function(np.c_[XX.ravel(), YY.ravel(), ZZ.ravel()])
plt.contourf(XX, YY, dec.reshape(XX.shape), levels = [dec.min(), 0, dec.max()], cmap=mglearn.cm2, alpha=0.5)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("특성 0")
plt.ylabel("특성 1")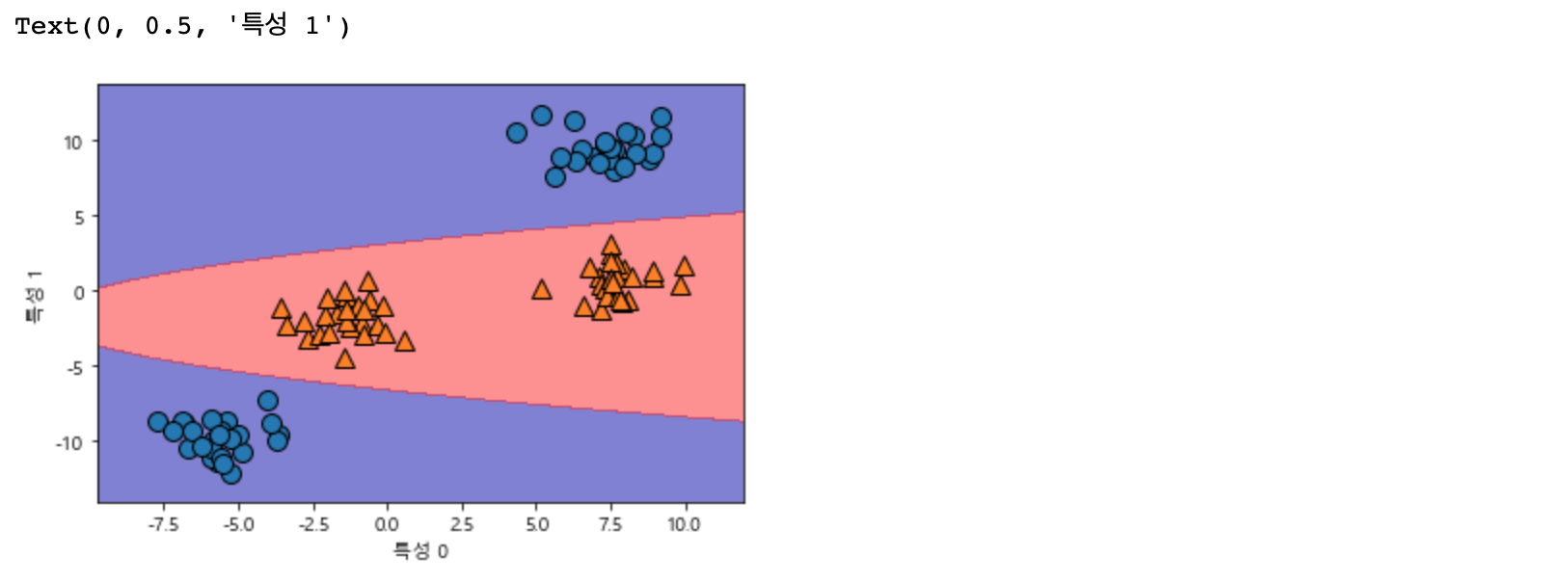
커널 기법 활용하기
앞서 비선형 특성을 추가하여 선형 모델을 조금 더 강력하게 만들어 보았습니다. 이전처럼 확실하게 어떤 특성에 비선형을 적용시켜야 할지 알고 있으면 좋겠지만, 보통은 어떤 특성을 추가해야 할지 모르고, 그렇다고 특성을 많이 추가하면 연산 비용(cpu, 메모리 사용 등)이 커지게 됩니다.
다행히도 수학적 기교를 통해 새로운 특성을 많이 만들지 않고도 고차원에서 분류기를 학습시킬 수 있습니다. 이를 커널 기법(kernel trick)이라고 합니다.
실제로 데이터를 확장하지 않고 확장된 특성에 대한 데이터 포인트들의 거리( 스칼라 곱 )를 계산합니다.
SVM에서 데이터를 고차원 공간에 매핑하는 방법은 두 가지가 있습니다. 차수를 더 늘린다
- 원래 특성의 가능한 조합을 지정된 차수까지 모두 계산(특성 1 제곱 * 특성 2 5제곱 등..) -> 다항식 커널
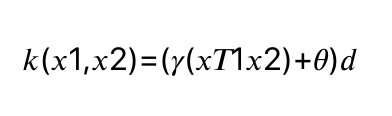
- RBF(radial basis function ) -> 가우시안 커널
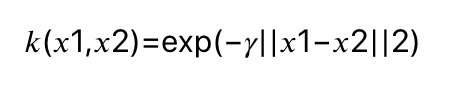
가우시안 커널은 차원이 무한한 특성 공간에 매핑하는 것으로, 모든 차수의 모든 다항식을 고려한다고 이해하면 됩니다. 하지만 특성의 중요도는 테일러급수 전개 때문에 고차항이 될수록 줄어듭니다.
복잡한가요? 실제로 수학적인 이론은 중요하지 않지만, RBF 커널을 사용한 SVM이 결정을 만드는 방법은 비교적 쉽게 요약이 가능합니다.
본격적 SVM 이해하기
학습이 진행되는 동안 SVM은 훈련 데이터 포인트가 두 클래스 사이의 결정 경계를 구분하는데 얼마나 중요한지를 배우게 됩니다.
일반적으로 훈련 데이터의 일부만 결정경계를 만드는데 영향을 주게 되는데, 바로 두 클래스 사이의 경계에 위치한 데이터 포인트들입니다.
이러한 데이터들을 서포트 벡터(support vector)라고 하며, 서포트 벡터 머신이 여기서 유래하였습니다.
새로운 데이터 포인트에 예측하려면 각 서포트 벡터와의 거리를 측정합니다. 분류에 대한 결정은 서포트 벡터까지의 거리에 기반하며 서포트 벡터의 중요도는 훈련 과정에서 학습하게 됩니다.(SVC객체의 dual_coef_ 속성에 저장)
데이터 포인트 사이의 거리는 가우시안 커널에 의해 계산됩니다.
𝑘(𝑥1,𝑥2)=exp(−𝛾||𝑥1−𝑥2||2) 수식으로 표현이 가능한데요, 여기서 𝑥1과 𝑥2는 데이터 포인트이며, ||𝑥1−𝑥2||는 유클리디안 거리, $\gamma$는 가우시안 커널의 폭을 제어하는 매개변수입니다.
이어서 forge 데이터셋에 SVM을 학습시켜 보겠습니다.
from sklearn.svm import SVC
X, y = mglearn.tools.make_handcrafted_dataset()
svm = SVC(kernel="rbf", C=10, gamma=0.1).fit(X, y)
mglearn.plots.plot_2d_separator(svm, X, eps=0.5)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
#서포트 벡터
sv = svm.support_vectors_
# dual_coef_의 부호에 의해 서포트 벡터의 클래스 레이블이 결정됨
sv_labels = svm.dual_coef_.ravel() > 0
mglearn.discrete_scatter(sv[:, 0], sv_labels, s = 15, markeredgewidth=3)
plt.xlabel("특성 0")
plt.ylabel("특성 1")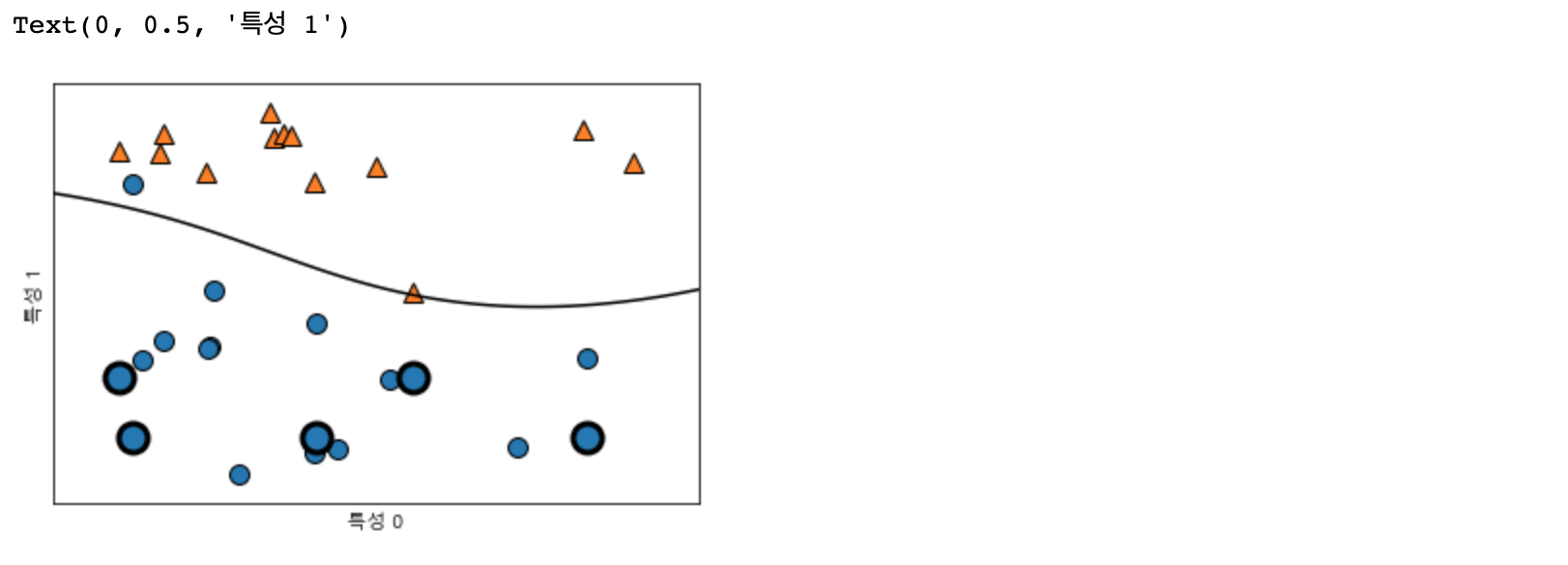
위 그림에서 결정경계는 검은색 선으로, 서포트 벡터는 굵은 테두리를 가진 데이터 포인트로 그려 보았습니다.
SVM의 핵심 매개변수는 C와 gamma 값으로, 자세히 살펴보겠습니다
SVM 매개변수 튜닝
1) 𝛾매개변수의 역할
gamma 매개변수는 𝛾 로 가우시안 커널 폭의 역수에 해당합니다. gamma 매개변수가 하나의 훈련 샘플에 미치는 영향의 범위를 결정합니다.
작은 값은 넓은 영역을 뜻하며 큰 값이라면 영향이 미치는 범위가 제한적입니다.
정리하자면 가우시안 커널의 반경이 클수록 훈련 샘플의 영향 범위도 커지게 됩니다. gamma는 0보다 범위가 커야 하기 때문에 가우시안 커널 함수의 값의 범위는 𝑒0 ~ 𝑒−∞ 사이입니다 즉 1~0 사이라고 볼 수 있는데요, 따라서 gamma 값이 적어질수록 데이터 포인트의 영향 범위가 커집니다.
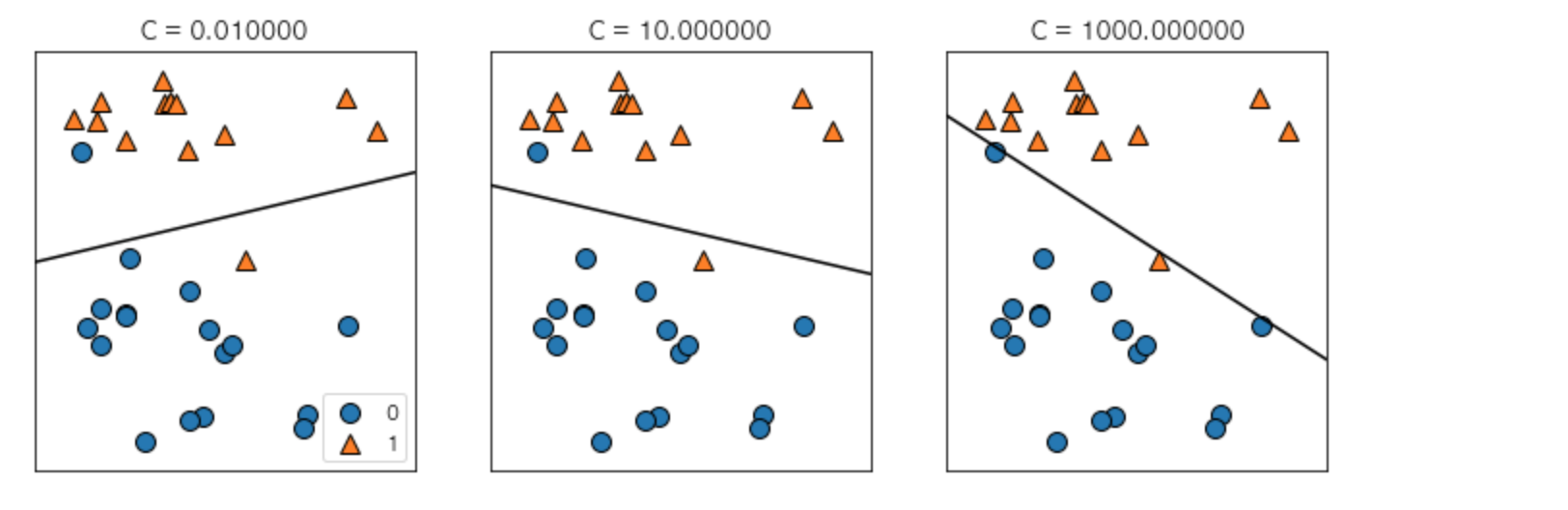
2) C 매개변수의 역할
C 매개변수는 선형 모델에서 사용한 것과 비슷한 규제 매개변수입니다. 이 매개변수는 각 포인트의 중요도(dual_coef_ 값)를 제한합니다.
C 매개변수를 다르게 했을 때 어떻게 변경되는지 살펴보겠습니다.
fig, axes = plt.subplots(3, 3, figsize=(15, 10))
for ax, C in zip(axes, [-1, 0, 3]) :
for a, gamma in zip(ax, range(-1, 2)):
mglearn.plots.plot_svm(log_C = C, log_gamma=gamma, ax=a)
axes[0, 0].legend(["클래스 0", "클래스 1", "클래스 0 서포트 벡터", "클래스 1 서포트 벡터"],
ncol=4, loc=(.9, 1.2))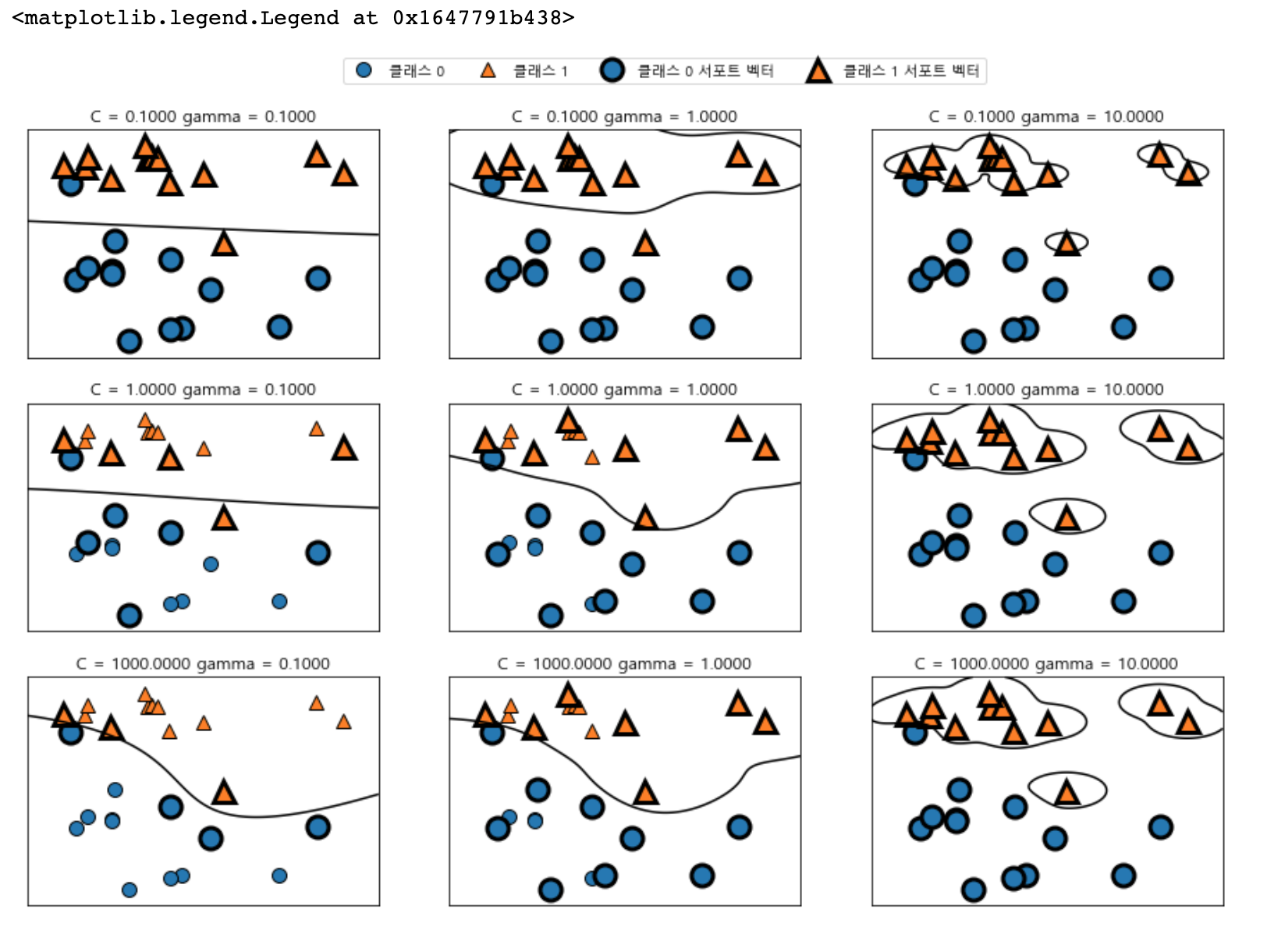
왼쪽에서 오른쪽으로 가면서 gamma 매개변수를 0.1에서 10으로 증가시킨 것부터 확인하면, gamma 값은 가우시안 커널의 반경을 크게 하여 많은 포인트들이 가까이 있는 것을 고려하는 모습이 보입니다.
그래서 왼쪽에 있는 결정 경계는 매우 부드러워지고, gamma값이 커질수록 결정 경계는 하나하나의 데이터 포인트에 민감해져 결정 경계를 각각 그리는 것이 확인됩니다.
작은 gamma 값이 결정 경계를 천천히 바뀌게 하므로 모델의 복잡도를 낮추게 됩니다. 반면에 gamma 값이 커지면 더욱더 복잡해집니다.
위에서 아래로는 C 매개변수를 0.1에서 1000까지 증가시켰습니다. 선형 모델에서처럼 작은 C는 매우 제약이 큰 모델을 만들고 각 데이터 포인트의 영향력이 작습니다. 왼쪽 위의 결정경계는 거의 선형에 가까우며 잘못 분류된 데이터 포인트가 경계에 영향을 주지 않는 것을 확인할 수 있습니다. 왼쪽 아래에서 볼 수 있듯이 C값을 증가시키면 이 포인트들이 모델에 큰 영향을 주게 되며 결정경계를 휘어서 정확하게 분류합니다.
RBF 커널 SVM을 유방암 데이터셋에 적용해 보겠습니다. 기본값 C=1, gamma=1/n_ features를 사용해 보도록 하겠습니다.
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer() #유방암 데이터 불러오기
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, random_state=0)
svc = SVC()
svc.fit(X_train, y_train)
print("훈련 세트 정확도: {:.2f}".format(svc.score(X_train, y_train)))
print("테스트 세트 정확도: {:.2f}".format(svc.score(X_test, y_test)))
훈련 세트에서는 완벽한 점수를 냈지만, 테스트 세트에서는 63% 의 정확도기 때문에 상당히 과대적합 된 것 같습니다. SVM은 꽤나 잘 작동하는 편이긴 하지만, 매개변수 설정과 데이터 스케일에 매우 민감합니다. 특히 입력 특성의 범위가 비슷해야 합니다. 각 특성의 최솟값과 최댓값을 로그 스케일로 나타내 보겠습니다.
plt.boxplot(X_train, manage_xticks=False)
plt.yscale("symlog")
plt.xlabel("특성 목록")
plt.ylabel("특성 크기")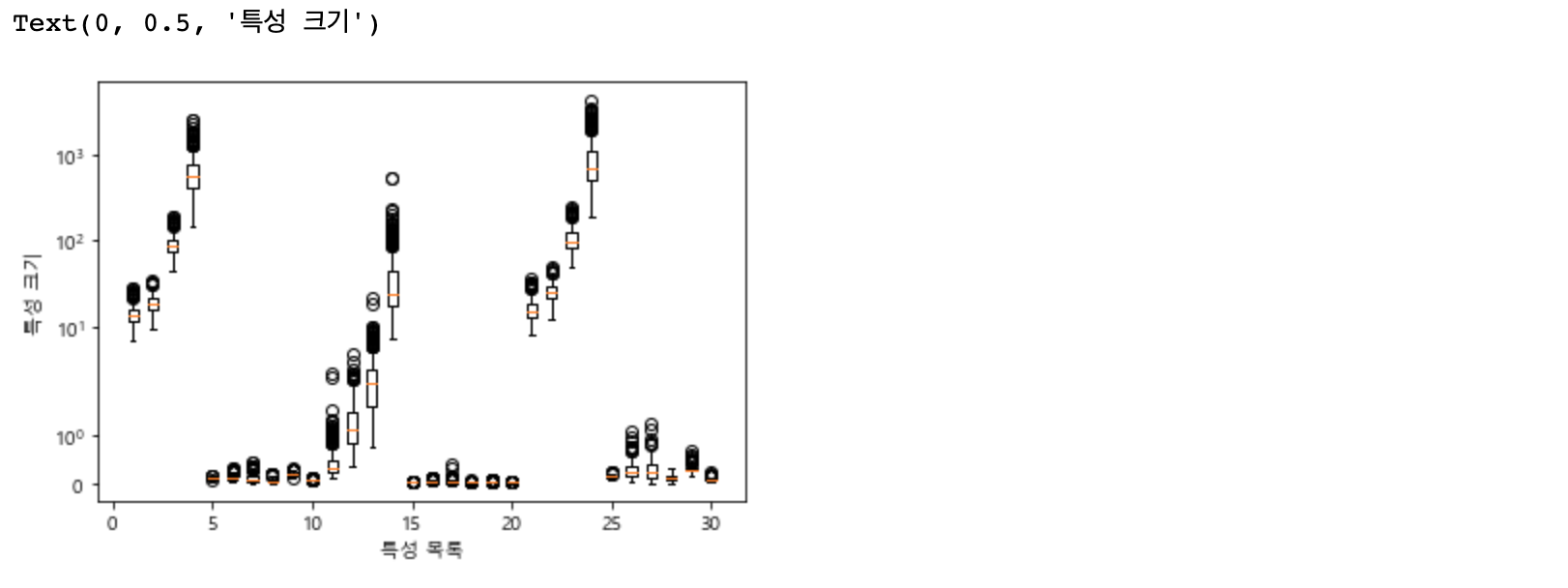
각 특성의 최댓값 최솟값을 확인해 보면 자릿수 자체가 다른 것이 확인됩니다. 이것이 선형 모델등에서도 문제가 될 수 있지만, 커널 SVM에서는 영향이 매우 큽니다. 이 문제를 해결하기 위해서는 각 특성들에 대해 전처리(pre processing) 작업이 필요합니다.
SVM을 위한 유방암 데이터셋 전처리
위의 문제를 해결하는 방법은 각 특성 값의 범위가 비슷해지도록 조정하는 것입니다. 커널 SVM에서는 모든 특성의 값을 0과 1 사이로 맞추는 방법을 사용합니다. MinMaxScaler 메소드를 사용할 수 있지만, 여기서는 우리가 직접 구현해 보겠습니다.
MinMaxScaler 메소드의 공식은 다음과 같습니다.
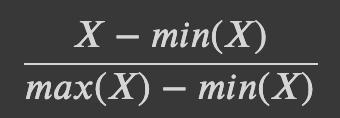
# 훈련 세트에서 특성별 최솟값 계산
min_on_training = X_train.min(axis=0)
# 훈련 세트에서 특성별 (최댓값 - 최솟값) 범위 계산
range_on_training = (X_train - min_on_training).max(axis=0)
# 훈련 데이터에 최솟값을 빼고 범위로 나누면
# 각 특성에 대해 최솟값은 0, 최댓값은 1입니다.
X_train_scaled = (X_train - min_on_training) / range_on_training
print("특성별 최소 값 :\n{}".format(X_train_scaled.min(axis=0)))
print("특성별 최대 값 :\n{}".format(X_train_scaled.max(axis=0)))
# 테스트 세트에도 같은 작업을 작용하지만
# 훈련 세트에서 계산한 최솟값과 범위를 사용합니다.
X_test_scaled = (X_test - min_on_training) / range_on_trainingsvc = SVC()
svc.fit(X_train_scaled, y_train)
print("훈련 세트 정확도:{:.3f}".format(svc.score(X_train_scaled, y_train)))
print("테스트 세트 정확도:{:.3f}".format(svc.score(X_test_scaled, y_test)))
전처리 과정을 통했더니 결과가 매우 크게 달라지는 것이 확인됩니다. 하지만 100% 정확도에서 조금 멀어졌지만 두 결과가 매우 비슷하기 때문에 확실히 과소적합된 상태라고 생각됩니다. 여기서 C나 gamma 값을 증가시켜 조금 더 복잡한 모델로 만들어 볼 수 있을 것 같습니다.
svc = SVC(C=1000)
svc.fit(X_train_scaled, y_train)
print("훈련 세트 정확도:{:.3f}".format(svc.score(X_train_scaled, y_train)))
print("테스트 세트 정확도:{:.3f}".format(svc.score(X_test_scaled, y_test)))
C 값을 증가시켰더니 모델의 성능이 97.2%로 상승하였습니다!
장단점과 매개변수
커널 서포트 벡터 머신은 매우 강력한 모델이며, 다양한 데이터셋에서 잘 작동합니다. SVM은 데이터의 특성이 몇 개 안 되더라도 복잡한 결정 경계를 만들 수 있으며 저 차원과 고차원의 데이터에 모두 잘 작동합니다.
하지만 샘플이 매우 많을 때는 잘 맞지 않습니다. 즉 10,000 개의 이상의 데이터셋에서는 잘 작동하지만, 100,000개 이상의 데이터셋에는 잘 작동하지 않을 수 있다는 측면이 있습니다. (속도와 메모리 관점에서..)
SVM의 또 다른 단점은 데이터의 전처리와 매개변수 설정에 생각보다 신경을 많이 써야 한다는 점입니다. 따라서 요즘에는 전처리가 거의 필요 없는 랜덤 포스트나 그래디언트 부스팅과 같은 트리 기반 모델을 애플리케이션에 많이 도입합니다. 또한 SVM은 수학 적인 관점에서도 모델을 설명하는 것 자체가 매우 어렵습니다.
!! BUT!!
모든 특성이 비슷한 단위이고( 예를 들어 픽셀의 컬러 강도 등...) 스케일이 비슷하면 SVM을 시도해 볼만합니다.
커널 SVM에서 중요한 매개변수는 규제 매개변수 C이고, 어떤 커널을 사용할지와 각 커널에 따른 매개변수입니다. 우리는 RBF 커널만 살펴봤지만 다른 커널도 많이 있습니다.
RBF 커널은 가우시안 커널 폭의 역수인 gamma 매개변수 하나를 가지고 있습니다. gamma와 C 모두 모델의 복잡도를 조정하며 둘 다 큰 값이 더 복잡한 모델을 만들어 냅니다. 따라서 연관성이 많은 이 두 개의 매개변수를 잘 설정하려면 C와 gamma를 함께 조정하는 것이 좋습니다.
'Programming > 특성 공학' 카테고리의 다른 글
| [Machine Learning] 앙상블 모델(Random Forest & Gradient Boosting) (0) | 2023.06.06 |
|---|---|
| [Machine Learning] 의사결정 트리(Decision Tree) 시각화 (0) | 2023.05.30 |
| [Machine Learning] 의사결정 트리(Decision Tree) (0) | 2023.05.23 |
| [Machine Learning] 다중 선형 분류 (0) | 2023.05.16 |
| [Machine Learning] 선형 이진 분류 (0) | 2023.05.09 |