유무디

지난 시간 역전파의 덧셈과 곱셈 노드에 대하여 알아보는 시간을 가졌습니다.

2024.02.22 - [Programming/Deep Learning] - [Python/DeepLearning] #10.4. 역전파) 덧셈 노드와 곱셈 노드

이번 시간에는 역전파의 완전 마지막! 활성화 함수 계층을 구현해 보도록 하겠습니다! 이 이상의 #10을 쪼개진 않겠습니다...

활성화 함수 계층 구현

드디어 지금 만든 계산 그래프를 신경망에 적용시켜 볼 수 있습니다!

여기에서는 신경망을 구성하는 층(계층) 각각을 클래스 하나씩으로 구현했는데요. 우선은 활성화 함수인 ReLU와 Sigmoid 계층을 구현해 보겠습니다!

ReLU 계층 만들기

먼저. 활성화 함수로 사용되는 ReLU의 수식은 다음과 같습니다.

위의 식을 미분하면 다음처럼 구할 수 있습니다.

순전파 때의 입력인 x가 0보다 크면 역전파는 상류의 값을 그래도 하류로 흘립니다.

반면에 순전파 때 x가 0 이하면 역전파 때는 하류로 신호를 보내지 않습니다.( 0을 보내기 때문입니다).

계산 그래프로는 다음 처럼 그릴 수 있겠네요!

그럼 본격적으로 ReLU 계층을 구현해 보도록 하겠습니다!

신경망 계층의 forward()와 backward() 함수는 넘파이 배열을 인수로 받는다고 가정합니다.

신경망 레이어 만들기

• ReLU
• Sigmoid
• Affine layer( 기하학 레이어 - Fully Connected, Dense )
• SoftMax + Loss layer

ReLU 구현

class ReLU:
  # mask : 순전파 시에 0이나 음수였던 인덱스를 저장하기 위함이다.
  # mask가 있어야 순전파 때 0이었던 부분을 역전파 때 0으로 만들어 줄 수 있다.
  def __init__(self):
    self.mask = None

  def forward(self, x):
    self.mask = (x <= 0)# 매개변수로 들어온 넘파이배열 x의 원소가  0이하인지 판단하기
    out = x.copy() # 원본 배열 복사
    out[self.mask] = 0 # 0보다 작은 원소들을 0으로 만들기

    return out

  # 순전파 때 음수였던 부분을 0으로 만든다.
  # 음수였었던 인덱스를 기억하고 있다가 (self.mask) 미분값 전달시에 해당 인덱스를 0으로 만든다.
  def backward(self, dout):
    dout[self.mask] = 0 # 상류에서 들어온 값에서 0보다 작은 값들에 대해 0으로 치환
    dx = dout # 완성된 ReLU 배열 리턴

    return dx

완성된 ReLU 계층을 np.array 배열을 넣어서 테스트해보겠습니다.

x = np.array([ [1.0, -0.5],
               [-2.0, 3.0] ])

print(x)

relu = ReLU()
relu.forward(x)

relu.mask

dx = np.array([ [-0.1, 4.0],
                [1.3, -1.1] ])

relu.backward(dx)

Sigmoid 계층 만들기

다시 한번 시그모이드 함수를 살펴보도록 하죠!

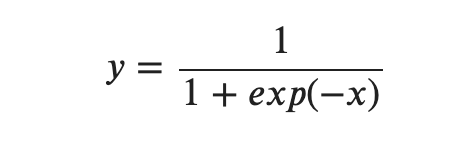
위 식을 계산 그래프로 그리면 다음과 같습니다.

X와 + 노드 말고 exp와 '/' 노드가 새롭게 등장했는데요, exp 노드는 𝑦=𝑒𝑥𝑝(𝑥) 계산을 수행하고, '/' 노드는 𝑦=1𝑥를 수행합니다. 그림과 같이 시그모이드의 계산은 국소적 계산의 순전파로 이루어집니다. 이제 역전파를 알아볼 텐데요, 각 노드에 대한 역전파를 단계별로 알아보도록 하겠습니다.

1단계

'/' 노드를 미분하면 다음과 같습니다.

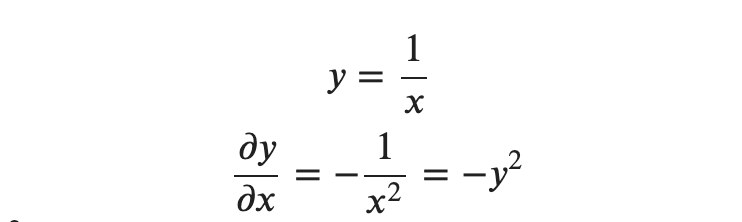
위처럼 상류에서 흘러 들어온 값에 −𝑦2(순전파의 출력을 제곱한 후 음수를 붙인 값)을 곱해서 하류로 전달시키게 됩니다. 계산 그래프에서는 다음과 같습니다.

2단계

'+' 노드는 상류의 값을 여과 없이 하류로 보냅니다. 계산 그래프의 결과는 다음과 같아집니다.

3단계

'exp'노드는 𝑦=𝑒𝑥𝑝(𝑥) 연산을 수행하며, 그 미분은 다음과 같습니다.

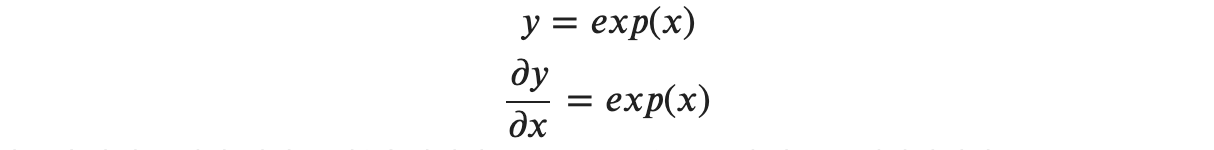
계산 그래프에서는 상류의 값에 순전파 때의 출력(이 예에서는 𝑒𝑥𝑝(−𝑥))을 곱해 하류로 전파합니다.

4단계

제일 마지막 X 노드는 순전파 때의 값을 서로 바꿔 곱합니다. 이 예에서는 -1을 곱하면 될 것 같습니다.

총 4 단계를 거쳐 Sigmoid 계층의 역전파를 계산 그래프로 완성해 보았습니다. 역전파의 최종출력인 ∂𝐿/∂𝑦*𝑦2*𝑒𝑥𝑝(−𝑥)) 값이 하류 노드로 전파됩니다. 그런데 ∂𝐿/∂𝑦*𝑦2*𝑒𝑥𝑝(−𝑥)를 순전파의 입력 𝑥와 출력 𝑦만으로 계산할 수 있다는 것을 알 수 있는데요, 따라서 계산 중간 과정을 모두 묶어서 다음처럼 단순한 그림으로 표현이 가능합니다.

또한 ∂𝐿/∂𝑦*𝑦2*𝑒𝑥𝑝(−𝑥)는 다음 처럼 정리할 수 있습니다.

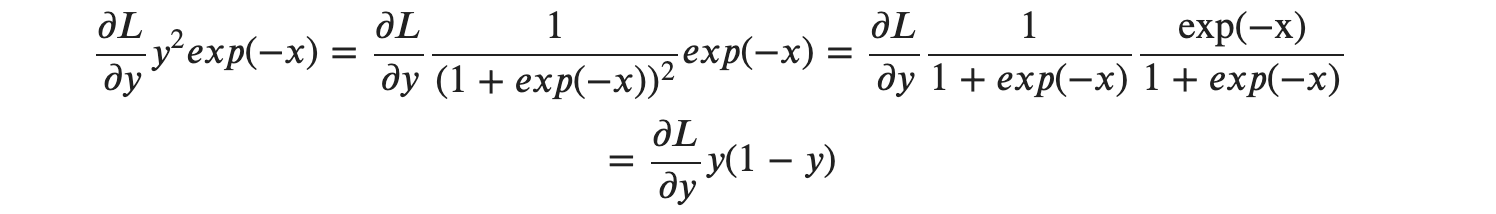
이처럼 Sigmoid 계층의 역전파는 순전파의 출력 y 만으로도 계산할 수 있습니다.

그렇다면, Sigmoid 계층을 파이썬으로 직접 만들어 보겠습니다.

Sigmoid 구현하기

class Sigmoid:
  def __init__(self):
    self.out = None

  # 순전파
  def forward(self, x):
    out = 1 / ( 1 + np.exp(-x) )
    self.out = out

    return out

  # 역전파
  def backward(self, dout):
    dx = dout * self.out * (1.0 - self.out)
    return dx

이 구현은 단순히 순전파의 출력을 인스턴스 변수 out에 보관했다가, 역전파 계산 때 그 값을 사용합니다.

지금까지 역전파의 단계별 구현을 해보았습니다. 

다음 시간에는 오차역전파의 Affine/Softmax 계층 신경망의 순전파에 대하여 구현해 보도록 하겠습니다.

지난 시간, 수식을 통한 오차역전파법에 대하여 이해해 보았습니다.

2024.02.08 - [Programming/Deep Learning] - [Python/DeepLearning] #10.2. 역전파) 수식을 통한 오차역전파법 이해

이번 시간에서는 계산 그래프를 통한 역전파에 대하여 알아보도록 하겠습니다!

오차역전파법을 위한 계산 그래프

일전에 수식으로 풀어본 오차역전파법은 수학을 오랫동안 놓았거나 수식으로만 생각하면 본질을 놓칠 우려가 있습니다. 이번에 우리가 해볼 내용은 계산 그래프를 이용해 오차역전파법을 이해하는 것인데요, 수식으로 오차역전파법을 이해하는 것보다는 약간은 부정확할 수 있으나 최종적으로는 수식으로 알아본 오차역전파법을 이해할 수 있고, 실제 코드 구현까지 해보도록 하겠습니다. 계산 그래프로 설명한다는 아이디어는 안드레 카패스의 블로그 또 그와 페이페이 리 교수가 진행한 스탠퍼드 대학교 딥러닝 수업 CS321n을 참고했습니다.

계산 그래프(computational graph)는 계산 과정을 그래프로 그려낸 것입니다. 그래프는 우리가 잘 아는 그래프 자료 구조 형태로 되어 있으며, 처음에 쉽게 접근하기 위해 계산 그래프를 통한 간단한 문제를 풀어보도록 하겠습니다. 먼저 익숙해지자!라는 이야기입니다. 예를 들어 다음과 같은 예시가 있다고 하죠, "A라는 사람이 1개 100원인 사과를 2개 샀습니다. 이때 지불 금액을 구하세요, 단 소비세 10%가 부과됩니다."라는 예시를 계산그래프로 표현하면 다음과 같아집니다.

처음에 사과의 100원이 'x 2' 노드로 흘러 200원이 된 다음 소비세 계산을 위해 'x 1.1' 노드를 거쳐 최종적으로는 220원이 됩니다. 위 그래프에 따르면 최종 답은 220원이 된다는 사실을 알 수 있네요 위의 그림에서는 계산 노드를 각각 'x 2', 'x 1.1'로 표현했지만 '2'와 '1.1'을 각각 사과의 개수와 소비세에 대한 변수가 되기 때문에 따로 빼서 다음과 같이 표기할 수 있습니다.

그럼 다음 문제를 풀어 보도록 하겠습니다.

"A가 사과를 2개, 귤을 3개 샀습니다. 사과는 1개에 100원, 귤은 1개 150원입니다. 소비세가 10% 부과될 때 A가 지불해야 할 금액은?" 위 문제도 계산그래프로 풀어볼 수 있습니다. 이때의 계산 그래프는 다음과 같겠네요!

위 문제에서는 새로운 노드인 덧셈 노드가 추가되었습니다. 덧셈 노드가 추가되어 사과의 가격과 귤의 가격을 합치는 모습이 보이고 있습니다. 왼쪽에서 오른쪽으로 순차적으로 계산을 끝내고 제일 마지막에 1.1을 곱하면 우리가 원하는 값인 715원이 나오고 끝나게 됩니다. 계산 그래프를 이용한 문제풀이는 다음과 같이 해석할 수 있습니다.

1. 계산 그래프를 구성
2. 그래프에서 계산을 왼쪽에서 오른쪽으로 진행

이처럼 '계산을 왼쪽에서 오른쪽으로 진행'하는 단계를 순전파(forward propagation)라고 합니다. 순전파는 계산 그래프의 출발점부터 종착점으로의 전파단계를 그려줍니다. 역전파(backword propagation)는 무엇일까요? 바로 '오른쪽에서 왼쪽으로 전파되는 단계를 의미합니다!

계산 그래프의 특징은 '국소적 계산'을 전파함으로써 최종 결과를 얻는다는 점에 있습니다. 여기서 '국소적'이란, "자신과 직접 관계된 작은 범위"를 의미하는데, 뭔가 떠오르지 않으시나요? 수학으로 따지면 바로 편미분을 의미한다는 것입니다. 즉, 국소적 계산은 전체에서 어떤 일이 벌어지든 상관없이 자신과 관계된 정보만을 토대로 결과를 낼 수 있다는 이야기입니다. 구체적인 예를 들어 보겠습니다. 여러분이 마트에서 사과 2개를 포함한 여러 가지의 물품들을 구매하는 상황을 구해보겠습니다. 그렇다면 사과에 대한 국소적 계산을 진행한다고 이해할 수 있는데요, 그래프로 확인해 보겠습니다.

위 그림에서 여러 식품을 구매하여( 복잡한 계산을 하여) 4,000원이라는 금액이 나왔고, 여기에 사과 가격인 200원을 더해 총 4,200원이 나왔습니다. 이는 '사과에 대한 국소적 계산'이기 때문에, 4,000원이 어떻게 나왔는지는 전혀 신경 쓸게 없다는 이야기가 됩니다. 그냥 단순히 복잡한 계산의 결과물인 4,000원과 사과의 가격인 200원을 더해 4,200을 알아내면 된다는 것이죠. 중요한 점은 계산 그래프는 이처럼 국소적 계산에 집중한다는 것입니다. 전체 계산 자체가 아무리 복잡해도 각 단계에서 하는 일은 해당 노드의 '국소적 계산'일뿐입니다. 국소적 계산은 단순하지만 그 결과를 전달함으로써 전체를 구성하는 복잡한 계산을 해낼 수 있습니다. 마치 자동차 조립을 하는 것과 비슷한데요, 각각의 부품을 복잡하게 만들어 내고, 최종적으로 합쳐 차를 완성하는 단계라고 볼 수 있습니다.

계산 그래프를 사용하는 이유

계산 그래프의 이점은 무엇일까요? 바로 국소적 계산입니다. 전체가 아무리 복잡해도 각 노드에서는 단순한 계산에 집중하여 문제를 단순화시킬 수 있기 때문이지요, 또한 계산 그래프는 중간 계산 결과를 모두 보관할 수 있습니다. 에지에 저장되어 있는 숫자들이 그것을 의미하고 있지요, 하지만 이것 때문에 계산 그래프를 사용하진 않습니다! 계산 그래프를 사용하는 가장 큰 이유는 역전파를 통해 '미분'을 효율적으로 계산할 수 있기 때문입니다.

계산 그래프의 역전파 첫 번째 문제에 대한 계산 그래프는 사과 2개를 사서 소비세를 포함한 최종 금액을 구하는 것이었습니다. 여기서 새로운 문제를 제시해 보겠습니다. "사과 가격이 오르면 최종 금액에 어떠한 영향을 미칠 것인가?"가 문제입니다. 즉 이는 사과 가격에 대한 지불 금액의 미분을 구하는 문제에 해당됩니다. 사과 값을 x로, 지불 금액을 L이라 했을 때

로 표현이 가능하다는 것이죠, 즉 이 미분값은 사과 값이 '아주 조금' 올랐을 때 지불 금액이 얼마나 증가하느냐를 표시한 것입니다. 즉, '사과 가격에 대한 지불 금액의 미분' 같은 값은 계산 그래프에서 역전파를 하면 구할 수 있게 됩니다. 다음 그림에서는 계산 그래프 상의 역전파에 의해 미분을 구할 수가 있습니다. 아직 역전파가 어떻게 이뤄지는지에 대해서는 이야기하지 않았습니다!

위 그림에서 굵은 화살표로 역전파를 표현해 보았습니다. 이 전파는 각각 노드에 대한 국소적 미분을 전달합니다. 즉, 들어오고 있는 사과의 개수나 소비세에 대한 국소적으로 미분을 진행하였기 때문에, 소비세와 사과의 개수 같은 변수에 대한 미분만 진행했다는 이야기입니다. 그리고 그 미분값은 화살표 방향으로 적어내고 있습니다. 이 예에서 역전 파는 오른쪽에서 왼쪽으로 '1 -> 1.1 -> 2.2' 순으로 미분값을 전달하고 있습니다. 이 결과로부터 알 수 있는 사실은 '사과 가격에 대한 지불금액이 미분'값은 2.2라는 것을 알 수 있게 됩니다. 즉, 사과 가격이 1원 오르면 최종 가격은 2.2원 오른다는 것이죠. 여기에서는 사과 가격에 대한 미분만 구했지만, '소비세에 대한 지불 금액의 미분'이나 '사과 개수에 대한 지불 금액의 미분'도 같은 순서로 구해낼 수가 있습니다. 그리고 그때는 중간까지 구한 미분 결과를 공유할 수 있어서 다수의 미분을 효율적으로 계산할 수 있습니다. 이처럼 계산 그래프의 이점은 순전파와 역전파를 활용해서 각 변수의 미분을 효율적으로 구할 수 있다는 것입니다.

연쇄법칙과 계산 그래프

연쇄법칙 계산을 계산 그래프로 나타낼 수 있습니다. 2 제곱 계산을 '**2' 노드로 나타내면 다음과 같습니다.

오른쪽에서 왼쪽으로 신호가 전파되는 모습을 볼 수 있습니다. 역전파에서의 계산 절차는 노드로 들어온 입력 신호에 그 노드의 국소적 미분인 편미분을 곱한 후 다음 노드로 전달합니다. 예를 들어 **2 노드에서의 역전파를 보면 입력은 ∂𝑧∂𝑧이며, 이에 대한 국소적 미분인 ∂𝑧∂𝑡를 곱해 다음 노드로 넘깁니다. 맨 왼쪽의 역전파를 보면 x에 대한 z의 미분이 연쇄법칙에 따라서

가 된다는 사실을 알아낼 수 있고, 이를 계산하면

가 된다는 사실을 알아낼 수 있습니다.

지금까지 아주아주 긴 오차역전파법을 위한 계산 그래프를 위한 이해를 수식으로 알아보았습니다! 다음 세션을 통해 최종적으로 코드 구현을 해보겠습니다.

지난 블로그, 행렬과 신경망에 대하여 알아보았습니다.

2023.08.30 - [Programming/Deep Learning] - [Python/DeepLearning] #5. 행렬과 신경망

이번 시간에는 신경망의 출력층에 대하여 알아보고 설계를 해보도록 하겠습니다~!

신경망의 사용처

신경망은 분류와 회귀 모두 사용할 수 있습니다.

다만 둘 중 어떤 문제냐에 따라 출력층에서 사용하는 활성화 함수가 달라집니다!

일반적으로 회귀에서는 항등함수, 분류에서는 소프트맥스 함수를 사용합니다.

항등 함수(Identity Function)와 소프트맥스 함수(Softmax Function) 구현해 볼까요?

출력층의 활성화 함수

• 이진 분류(Binary Classification) : 𝑠𝑜𝑓𝑡𝑚𝑎𝑥, 𝑠𝑖𝑔𝑚𝑜𝑖𝑑 함수를 주료 사용
• 다중 분류(Mulitple Classification) : 𝑠𝑜𝑓𝑡𝑚𝑎𝑥

보통 전천후 함수로 𝑠𝑜𝑓𝑡𝑚𝑎𝑥 함수를 주로 사용하는 추세이고, 𝑠𝑖𝑔𝑚𝑜𝑖𝑑를 출력층의 활성화 함수로 사용할 때는 출력층의 뉴런은 한 개로 설정한다.

출력층에서 사용하는 활성화 함수인 항등함수는 정말 쉽습니다.

일전에도 살펴봤지만, 입력한 값을 그대로 출력값으로 내보내면 됩니다.

한편, 분류에서 사용되는소프트맥스의 식은 다음과 같습니다.

여기서 𝑒𝑥𝑝(𝑥))는𝑒𝑥을 뜻하는 지수함수입니다.

𝑛은 출력층의 뉴런의 개수이며, 𝑦𝑘는 출력층 뉴런의𝑘 번째 출력을 의미합니다.

소프트맥스 함수의 분자는 출력층으로 입력되는 입력값 𝑎𝑘로 구성되며, 분모는 모든 입력값의 지수 함수의 합으로 구성됩니다.

계속해서 소프트맥스 함수를 직접 구현해 보도록 하겠습니다. 먼저 원리부터 살펴보겠습니다.

# softmax 함수 구현하기 - 원리
import numpy as np

a = np.array([0.3, 2.9, 4.0]) # 입력 신호

# 분자 계산
exp_a = np.exp(a) # 모든 입력 신호에 대한 지수 함수 적용 (분자 값)
print("각 입력 함수에 대한 지수 함수 적용 결과 : {}".format(exp_a))

# 분모 계산
sum_exp_a = np.sum(exp_a)  # 분모가 될 모든 입력 신호에 대한 지수 함수의 합
print("softmax 함수의 분모값 : {}".format(sum_exp_a))

# 소프트맥 계산, numpy 배열 형태로 등장하기 때문에 한꺼번에 계산 가능
y = exp_a / sum_exp_a
print("softmax 결괏값 : {}".format(y)) # 각 입력 값 별 softmax 결괏값

각 입력 함수에 대한 지수 함수 적용 결과 : [ 1.34985881 18.17414537 54.59815003]
softmax 함수의 분모값 : 74.1221542101633
softmax 결괏값 : [0.01821127 0.24519181 0.73659691]

print("softmax 결괏값의 총 합 : {}".format(np.sum(y)))

softmax 결괏값의 총 합 : 1.0

복잡해 보였던 소프트맥스 함수의 식을 파이썬으로 표현해 보았습니다.

생각보다 어렵진 않죠? 그럼 직접적으로 소프트맥스 함수를 구현해 보겠습니다.

# 𝑠𝑜𝑓𝑡𝑚𝑎𝑥  함수 직접 구현
def softmax(a):
  exp_a = np.exp(a)
  sum_exp_a = np.sum(exp_a)
  y = exp_a / sum_exp_a

  return y

softmax(a)

𝑠𝑜𝑓𝑡𝑚𝑎𝑥 함수 튜닝하기

소프트맥스 함수는 지수 함수를 사용합니다.

따라서 입력 값이 약간만 커져도 굉장히 큰 값을 연산해야 합니다.

예를 들어 𝑒10=20,000 정도이고, 𝑒100은 0이 40개 넘는 수, 보통 𝑒10001000은 무한대를 의미하는 𝑖𝑛𝑓를 만들어 냅니다.

또한 이렇게 큰 값으로 나눗셈을 하면 수치가 '불안정'해지기 마련입니다.

따라서 이 문제를 해결하기 위해 소프트맥스 함수를 약간 개선해 줄 필요가 있습니다.

log의 개념을 활용하면 손쉽게 처리가 가능합니다!

위 식의 전개 과정은 다음과 같습니다.

1. 분자와 분모 모두에 𝐶라는 임의의 정수를 곱합니다. 

2. 𝐶를 지수 함수 exp 안으로 옮겨서 𝑙𝑜𝑔𝐶로 만들어 줍니다. 

3. 𝑙𝑜𝑔𝐶를 𝐶′′라는 새로운 기호로 바꿔 줍니다.

소프트맥스 함수의 지수 함수를 계산할 때 어떤 정수를 더하거나 빼도 결과는 바뀌지 않습니다.

여기서 𝐶′에 어떤 값을 대입해도 상관은 없지만, 오버플로를 막을 목적으로는 입력 신호들 중 최댓값을 이용하는 것이 일반적입니다.

다음 예를 살펴보겠습니다.

big_a = np.array( [1010, 1000, 990] )
print(softmax(big_a))                    # 소프트맥스 함수 계산

너무 큰 숫자를 계산하는 바람에 모든 값에 NaN 이 출력되는 것이 확인됩니다.

입력 특성의 최댓값을 𝐶′으로 집어넣어서 계산해 보겠습니다.

overflow 발생 원인

𝑒𝑥𝑝함수는 지수함수이다. 𝑒10 은 약 20,000이고,𝑒100은 0이 40개 넘어가고, 𝑒1000은 컴퓨팅 시스템에서 무한대를 의미하는 𝑖𝑛𝑓를 의미한다.

해결하기 위해서는 𝑙𝑜𝑔를 활용한다. 참고로 지수함수에서의 𝑙𝑜𝑔는 뺄셈을 의미한다.

1. 분자와 분모에 𝐶라는 임의의 정수를 곱합니다.
2. 𝐶를 지수 함수 𝑒𝑥𝑝안으로 옮겨서 𝑙𝑜𝑔𝐶로 만들어 준다.
3. 𝑙𝑜𝑔𝐶를 𝐶′′이라는 새로운 기호로 바꿔준다.

# 보통 상수 C는 입력값 중에 제일 큰값으로 선정한다.
c = np.max(big_a)
print(big_a-c)

print(np.exp(big_a-c) / np.sum(np.exp(big_a-c)))

정상적으로 잘 구해지는 것이 확인됩니다!

이를 토대로 소프트맥스 함수를 다시 정의해 보겠습니다.

def softmax(a):
  c = np.max(a) # 상수 c 구하기( 입력의 최댓값 ) c=1010
  exp_a = np.exp( a - c ) # a + log C ; 각 원소마다 차를 구함 " overflow 대책 "

  sum_exp_a = np.sum(exp_a)
  y = exp_a / sum_exp_a

  return y

big_y = softmax(big_a)
print("softmax 결과 : {}".format(big_y))
print("softmax 총합 : {}".format(np.sum(big_y)))

𝑠𝑜𝑓𝑡𝑚𝑎𝑥 함수의 특징

소프트맥스 함수를 사용하면 다음과 같이 신경망의 출력을 계산할 수 있습니다.

y = softmax(a)
print("softmax 결과 : {}".format(y))
print("softmax 총합 : {}".format(np.sum(y)))

소프트맥스 함수 결괏값 배열의 원소들은 항상 0과 1 사이의 실수입니다.

가장 중요한 성질은 소프트맥스 함수의 출력 총합은 1이라는 것입니다.

총합이 1이 된다는 점이 소프트맥스 함수의 가장 중요한 성질입니다.

이 성질 덕분에 소프트맥스 함수의 출력을 '확률'로 재해석할 수 있습니다.

위의 결과물을 예시로 들자면, "y [0]의 확률은 약 1.8%, y [1]의 확률은 24.5%, y [2]의 확률은 73.7%로 해석 가능하며,

• 약 74% 확률로 2번째 클래스, 25%의 확률로 1번째 클래스, 1%의 확률로 0번째 클래스이다.

라는 식으로 확률적인 결론을 낼 수 있게 됩니다.

즉, 소프트맥스 함수를 이용함으로 인해 문제를 확률적(통계적)으로 대응할 수 있게 되는 것입니다.

여기서 주의할 점으로, 소프트맥스 함수를 적용해도 각 원소의 대소 관계는 변하지 않습니다.

이는 지수 함수 𝑦=𝑒𝑥𝑝(𝑥)가 단조함수( 정의역 원소 a, b가𝑎≤𝑏 일 때, 𝑓(𝑎)≤𝑓(𝑏)가 되는 함수)이기 때문입니다.

실제로 앞의 예에서의 a의 원소들 사이의 대소 관계가 y의 원소들 사이의 대소 관계로 그대로 이어지는 것이 확인됩니다.

신경망을 이용한 분류에서는 일반적으로 가장 큰 출력을 내는 뉴런에 해당하는 클래스로만 인식됩니다.

그리고 소프트맥스 함수를 적용해도 출력이 가장 큰 뉴런의 위치는 변화되지 않습니다.

결과적으로 신경망으로 분류할 때는 출력층의 소프트맥스 함수를 생략해도 됩니다.

실제 현업에서도 지수 함수 계산에 드는 자원 낭비를 줄이고자 소프트맥스 함수를 생략하는데요, 그렇다면 왜 소프트맥스 함수를 배웠을까요?

이는 기계학습의 문제 풀이는 학습과 추론 두 단계를 거치기 때문입니다.

학습 단계에서 모델을 학습하고, 추론 단계에서 앞서 학습한 모델로 미지의 데이터에 대해서 추론(분류)을 수행하게 됩니다.

이때, 추론 단계에서는 소프트맥스 함수를 생략하는 것이 일반적입니다만, 신경망을 학습시킬 때는 출력층에서 소프트맥스 함수를 사용하게 됩니다. 신경망을 학습시킨다는 개념은 조금 나중에 이야기하도록 하겠습니다.

다음 블로그에서는 출력층의 뉴런 수 정하는 방법과 Tensorflow MNIST 데이터를 불러와서 형상 다루는 방법에 대하여 알아보도록 하겠습니다!

지난 블로그에서는 차원의 수에 관련하여 알아보았습니다.

2023.08.23 - [Programming/Deep Learning] - [Python/DeepLearning] #4. 다차원 배열의 계산

이번에는 행렬과 신경망에 대하여 알아보도록 하겠습니다.

신경망의 입력과 가중치

신경망으로 들어오는 입력값은 여러 개고, 입력값에 해당하는 가중치도 여러 개입니다.

만약 두 개의 입력값이 있고, 3개의 유닛으로 입력값들을 보낸다면 어떻게 해야 할까요?

편향과 활성화 함수가 없는, 아주 간단한 신경망을 만들어 보겠습니다.

import numpy as np

X = np.array([1, 2])
print("입력값 X의 shape : {}".format(X.shape)) # 입력값의 개수는 두개

W = np.array([[1,3,5], [2,4,6]])             # 3개의 유닛으로 전달 되어지는 입력값에 대한 각각의 가중치 행렬
print("가중치 W의 shape : {}".format(W.shape))

Y = np.dot(X, W)                             # 행렬의 내적을 이용한 결과 Y 계산
print("출력값 Y : \n{}".format(Y))

np.dot 함수 한 번으로 단번에 결과 Y를 낼 수 있습니다. 이번엔 3층 신경망을 구현해 보도록 하겠습니다. 입력값은 두 개(𝑥1, 𝑥2)가 있고, 첫 번째 은닉층(1층)은 3개, 두 번째 은닉층(2층)은 2개, 출력층(3층)은 2개의 뉴런으로 구성합니다. 코드를 작성하기 전에, 각 수식을 따져보기 위해 다음과 같은 규칙을 정하겠습니다. 가중치 𝑤를 기준으로 작성해 보면 다음과 같습니다.

 

를 봤을 때 𝑤(1)은 1층의 가중치, 즉 층의 숫자를 의미하고, 아래에 있는 𝑤1212에서 앞의 1은 𝑤가 흘러가는 다음 층의 1번째 뉴런, 뒤에 있는 2는 앞층의 2번째 뉴런을 의미합니다.

위의 식을 토대로 첫 번째 층(입력층)의 가중치와 편향을 받은 첫 번째 은닉 유닛의 결과를 𝑎(1)1(1) 1이라고 가정해 보겠습니다. 이때 해당 뉴런의 계산 식은 다음과 같이 볼 수 있습니다. 편향도 같이 1로 입력이 된다고 생각해 보겠습니다.

 

여기에서 행렬의 내적을 이용해 생각해 볼 수 있겠습니다. 총 3개의 은닉 유닛이 존재하기 때문에 각 첫 번째 층을 행렬로 만들어 일반화시켜보면 다음과 같습니다.

 

각 행렬의 값은 다음과 같습니다.

복잡하지만 어려울 것 없습니다! 기본 선형 함수를 사용했던 뉴런 하나를 여러 개 쌓은 것뿐이고, 거기에 번호를 붙인 것뿐입니다. 본격적으로 첫 번째 은닉층에 대한 구현을 해보겠습니다.

X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])  # 2개씩 입력을 받는 3개의 뉴런
B1 = np.array([0.1, 0.2, 0.3])                     # 3개의 뉴런에 더해질 편향들

print("입력값 X의 shape : {}".format(X.shape))
print("첫 번째 층 가중치 W1의 shape : {}".format(W1.shape))
print("편향 B1의 shape : {}".format(B1.shape))

# Result
A1 = np.dot(X, W1) + B1
print("첫 번째 층의 각 노드의 계산값 : {}".format(A1))

여기서 끝나는 게 아닌, 계산된 최종 결과물에 활성화 함수를 사용해 주면 완벽한 신경망 뉴런이 됩니다.

일전에 했었던 시그모이드 함수를 적용시켜 보겠습니다. 첫 번째 층의 결과물 행렬인 A1에 활성화 함수 시그모이드 함수를 적용시킨 결과물은 Z1이라고 칭하겠습니다.

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# Result array
Z1 = sigmoid(A1)
print("시그모이드 적용 후 : {}".format(Z1))

그다음은 1층에서 2층으로 가는 과정입니다.  그럼, 앞서했던 것처럼 2층은 이렇게 표현되겠죠?

W2 = np.array([[0.1, 0.4],
               [0.2, 0.5], 
               [0.3, 0.6]])                # 3개의 입력을 받는 2개의 뉴런
               
B2 = np.array([0.1, 0.2])

print("1층의 결과물 Z1의 shape : {}".format(Z1.shape))
print("1층에서 2층으로 넘어가기 위한 가중치 W2 shape : {}".format(W2.shape))
print("2층 노드의 편향들 B1의 shape : {}".format(B2.shape))

A2 = np.dot(Z1, W2) + B2                    # 1층에서 넘어온 값에 가중치 및 편향 계산 추가
Z2 = sigmoid(A2)                            # 시그모이드 함수 적용
print("시그모이드 적용 후 : {}".format(Z2))

1층의 출력 Z1의 2층의 입력이 된다는 점 빼고는 위에서 구현한 코드와 똑같습니다.

numpy 배열만 사용해도 충분히 망을 구축할 수 있을 것 같습니다. 마지막으로 2층에서 출력층으로의 신호 전달입니다.

은닉층에서는 시그모이드 활성화 함수를 사용했지만, 출력층에서는 항등함수, 교차 엔트로피, 소프트맥스 함수 등을 사용해서 결과를 냅니다. 여기에서는 입력값을 그대로 출력하는 항등함수를 활용해 보겠습니다.

굳이 구현할 필요는 없지만, 지금까지 만들어 왔던 패턴과 일치하기 위해 항등함수를 만들겠습니다.

# 출력층
# 항등함수
def identity_function(x):
    return x

W3 = np.array([[0.1, 0.3], 
               [0.2, 0.4]])                     # 2개의 입력을 받는 2개의 뉴런
               
B3 = np.array([0.1, 0.2])

A3 = np.dot(Z2, W3) + B3
Y  = identity_function(A3)                      # Y = A3와 똑같음
print("출력층 결과 : {}".format(Y))

최종 구현 정리

3층 신경망에 대한 정리였습니다.

뉴런이 많아지기 때문에 각각을 행렬로 표현하였고, 각각의 뉴런들은 지금까지 봐왔던 선형함수를 사용하며, 그 결과를 활성화 함수에 넣어 유동적인 값을 가질 수 한다는 것이 이번 구현의 핵심 포인트입니다.

출력층의 결과를 내기 위한 활성화 함수도 따로 있다는 사실이 잠깐 등장하였습니다.

def init_network():

    # 네트워크 초기화 과정
    # 네트워크가 초기화 되면 일반적으로 정규분포 * 0.01 정도의 랜덤값으로 초기화 한다.
    # 다른 방법으로 카이밍 He 초깃값 또는 Xavier 초깃값을 사용한다. (이때, 활성화 함수에 따라 달라진다!)
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])
    
    return network

# 순전파 과정
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    z1 = np.dot(x, W1) + b1
    a1 = sigmoid(z1)
    
    z2 = np.dot(a1, W2) + b2
    a2 = sigmoid(z2)
    
    z3 = np.dot(a2, W3) + b3
    y  = identity_function(z3)
    
    return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)

여기까지가 신경망의 순방향 구현은 끝입니다!

넘파이의 배열만 잘 사용해도 효율적인 신경망을 구현할 수 있습니다.

다음 블로그에서는 출력층 설계에 관하여 더 알아보도록 하겠습니다!