2023.05.23 - [Programming/특성 공학] - [Machine Learning] 의사결정 트리(Decision Tree)
[Machine Learning] 의사결정 트리(Decision Tree)
이번 포스팅에서는 의사결정 트리(Decision Tree)에 대하여 알아보도록 하겠습니다! 결정 트리(Decision Tree) 분류와 회귀 문제에 널리 사용하는 모델입니다. 기본적으로 결정 트리는 스무고개 놀이와
yuja-k.tistory.com
앞서, Decision Tree에 관한 개념과 알고리즘을 통해 구현해 보았습니다. 이번 블로그에서는 Decision Tree의 시각화 및 특성 중요도에 대하여 알아보고 결정 트리의 장단점에 대하여 알아보도록 하겠습니다.
트리 시각화 하기
트리 모듈의 export_graphviz 함수를 이용하면 트리를 시각화할 수 있습니다.
from sklearn.tree import export_graphviz
export_graphviz(tree, out_file="tree.dot", class_names=["악성","양성"],
feature_names=cancer.feature_names, impurity=False, filled=True)with open("tree.dot") as f:
dot_graph = f.read()
display(graphviz.Source(dot_graph))
트리를 시각화 함에 따라 알고리즘의 예측을 쉽게 할 수 있게 됐습니다. 깊이가 4만 되었는데도 불구하고 매우 복잡한데, 보통은 10이 정도의 깊이를 사용합니다. samples는 각 노드에 있는 샘플의 수를 의미하며, value는 클래스당 샘플 수를 제공합니다.
트리의 특성 중요도 ( Feature Importance )
전체 트리를 살펴보는 것은 힘든 일입니다. 대신 트리가 어떻게 작동하는지 요약하는 속성들을 사용할 수 있습니다. 가장 널리 사용되는 속성은 트리를 만드는 결정에 각 특성이 얼마나 중요한지를 평가하는 특성 중요도 이 값은 0과 1 사이의 숫자로, 각 특성에 대해 0은 전혀 사용되지 않았다는 것을 의미하고, 1은 완벽하게 타깃 클래스를 예측했다는 뜻이 됩니다.
print("특성 중요도 :\n{}".format(tree.feature_importances_))
def plot_feature_importances_cancer(model):
n_features = cancer.data.shape[1]
plt.barh(range(n_features), model.feature_importances_, align='center')
plt.yticks(np.arange(n_features), cancer.feature_names)
plt.xlabel("특성 중요도")
plt.ylabel("특성")
plt.ylim(-1, n_features)
plot_feature_importances_cancer(tree)
첫 번째 노드에서 사용한 특성인 worst radius 가 가장 중요한 특성으로 나타나는 것이 확인됩니다. 이 그래프는 첫 번째 노드에서 두 클래스( 악성, 양성 )를 꽤나 잘 나누고 있다는 것을 의미합니다.
feature_importance_의 값이 낮다고 아예 중요하지 않은 값은 아닙니다. 단지 트리가 그 특성을 선택하지 않은 것뿐이며 다른 특성이 동일한 정보를 지니고 있어서 일 수도 있습니다.
선형 모델의 계수와는 다르게 특성 중요도는 언제나 양수이며 특성이 어느 클래스를 지지하는지 ( 결정하는데 역할을 하는지 ) 알 수가 없습니다. 즉 특성 중요도의 값은 "worst radius"가 중요하다고 알려주지만, 이 특성이 양성을 의미하는지, 악성을 의미하는지는 알 수 없습니다.
사실 특성과 클래스 사이에는 간단하지 않은 관계가 있을 수 있기 때문에 다음 예를 들어 보겠습니다.
tree = mglearn.plots.plot_tree_not_monotone()
display(tree)
두 개의 특성과 두 개의 클래스를 가진 데이터셋을 표현하고 있습니다. X [1]에 있는 정보만 사용되었고, X [0]은 전혀 사용되지 않았습니다. 그런데 X [1]과 출력 클래스와의 관계는 단순히 비례나 반비례하지 않습니다. 즉 "X [1]의 값이 높으면 클래스 0이고 값이 낮으면 1"이라고 말할 수 없습니다.
결론적으로 데이터의 분포도와 트리에 사용된 특성을 참고하면서 트리에서 사용한 특성이 정말 중요한 특성인지, 혹시 놓친 특성은 없는지 살펴봐야 할 것 같습니다.
결정 트리 회귀
우리는 여기서 결정 트리를 가지고 분류에 대해서만 논하고 있지만 사실상 회귀에서도 비슷하게 적용됩니다. 회귀 트리의 사용법은 분류 트리와 매우 비슷합니다.
하지만 회귀를 위한 트리 기반의 모델을 사용할 때 확인 해 봐야 할 속성이 있습니다.
DecisionTreeRegressor( 그리고 모든 다른 트리 기반 회귀 모델 )는 외삽(extrapolation), 즉 훈련 데이터의 범위 밖의 포인트에 대해 예측을 할 수 없습니다.
import os
ram_prices = pd.read_csv(os.path.join(mglearn.datasets.DATA_PATH, "ram_price.csv"))
plt.semilogy(ram_prices.date, ram_prices.price)
plt.xlabel("년")
plt.ylabel("가격 ($/Mbyte)")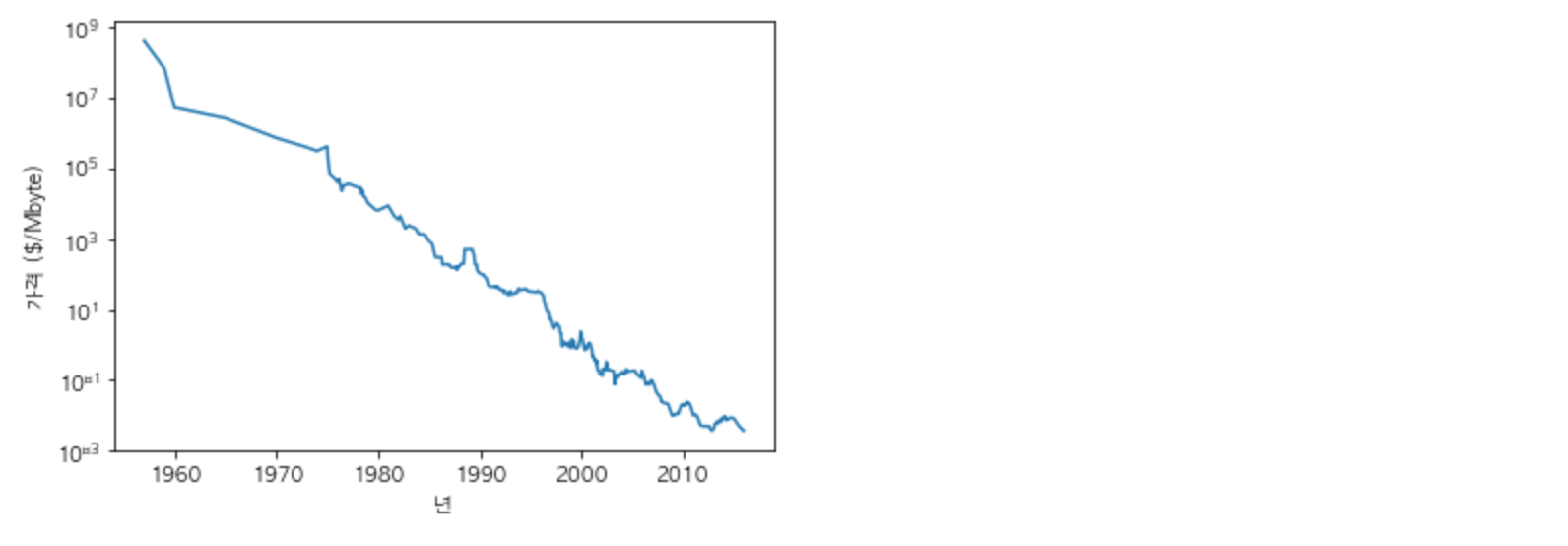
y축은 로그 스케일로써 선형적으로 그리기 좋기 때문에 비교적 예측이 쉬워집니다.
날짜 특성 하나만으로 램의 2000년도 전까지의 데이터로부터 2000년도 이후의 가격을 예측해 보겠습니다. 여기서는 간단한 두 모델인 DecisionTreeRegressor와 LinearRegression을 비교해 보도록 하겠습니다.
그래프 표현식을 위해 전체 데이터셋에 대해 예측을 수행하였지만, 테스트 데이터셋의 비교가 관심 대상입니다.
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression
# 2000년 이전을 훈련 데이터로, 2000년 이후를 테스트 데이터로
data_train = ram_prices[ram_prices.date < 2000]
data_test = ram_prices[ram_prices.date >= 2000]
# 가격 예측을 위해 날짜 특성만을 이용합니다.
X_train = data_train.date[:, np.newaxis]
# 데이터와 타깃 관계를 간단하기 위해 로그 스케일로 바꿉니다.
y_train = np.log(data_train.price)
tree = DecisionTreeRegressor().fit(X_train, y_train)
linear_reg = LinearRegression().fit(X_train, y_train)
# 예측은 전체 기간에 대해서 수행합니다.
X_all = ram_prices.date[:, np.newaxis]
pred_tree = tree.predict(X_all)
pred_lr = linear_reg.predict(X_all)
# 예측한 값의 로그 스케일을 되돌립니다.
price_tree = np.exp(pred_tree)
price_lr = np.exp(pred_lr)plt.semilogy(data_train.date, data_train.price, label="훈련 데이터")
plt.semilogy(data_test.date, data_test.price, label="테스트 데이터")
plt.semilogy(ram_prices.date, price_tree, label="트리 예측")
plt.semilogy(ram_prices.date, price_lr, label="선형 회귀 예측")
plt.legend()
두 모델은 확연한 차이를 보이고 있습니다. 선형 모델 ( 빨간 선 )은 우리가 이미 알고 있는 대로 데이터를 근사하여 직선을 2000년 이후 데이터를 꽤나 정확히 예측하고 있습니다. 하지만 트리 모델은 훈련 데이터를 ( 2000년도 이전 ) 완벽하게 예측합니다.
트리의 복잡도에 제한을 두지 않아서 저체 데이터셋을 모두 기억하기 때문입니다. 그러나 모델이 가진 데이터 범위 밖으로 나가면 단순히 마지막 포인트를 이용해 예측하는 것이 전부입니다.
트리 모델은 훈련 데이터 밖의 새로운 데이터를 예측할 능력이 없습니다. 이는 모든 트리 기반 모델의 공통적인 단점입니다.
장단점과 매개변수
결정 트리에서의 모델 복잡도를 조절하는 매개변수는 트리가 완전히 만들어지기 전에 멈추는 사전 가지치기 매개변수입니다. 우리는 실제 하나만 써 보았지만 3개의 매개변수가 있습니다.
- max_depth
- max_leaf_nodes
- min_sample_leaf
위의 매개변수 중 하나만 조절해도 과대적합을 막는데 충분합니다.
결정 트리의 장점
이전에 소개한 다른 알고리즘보다 나은 점은 총 두 가지로 정리가 가능합니다.
- 1) 만들어진 모델을 쉽게 시각화 할 수 있어서 비 전문가도 이해하기가 쉽습니다. ( 너무 크지 않다면...)
- 2) 데이터의 크기게 구애 받지 않습니다.
각 특성이 개별적으로 처리되어 데이터를 분할하는데 데이터 스케일의 영향을 받지 않으므로 결정 트리에서는 특성의 정규화나 표준화 같은 전처리 과정이 필요가 없습니다.
특히 특성의 스케일이 서로 다르거나 이진 특성과 연속적인 특성이 혼합되어 있을 때도 잘 작동합니다.
결정 트리의 단점
매개변수를 조절해 사전 가지치기를 사용함에도 불구하고 과대적합되는 경향이 있어 일반화 성능이 좋지 못합니다. 따라서 다음에 해볼 랜덤포레스트 - 앙상블 방법을 단일 결정 트리의 대안으로 흔히 사용합니다.
'Programming > 특성 공학' 카테고리의 다른 글
| [Machine Learning] 서포트 벡터 Support Vector Machine(SVM) (0) | 2023.06.13 |
|---|---|
| [Machine Learning] 앙상블 모델(Random Forest & Gradient Boosting) (0) | 2023.06.06 |
| [Machine Learning] 의사결정 트리(Decision Tree) (0) | 2023.05.23 |
| [Machine Learning] 다중 선형 분류 (0) | 2023.05.16 |
| [Machine Learning] 선형 이진 분류 (0) | 2023.05.09 |