이번 블로그는 선형 모델에 대하여 알아보도록 합시다.
선형 모델은 매우 오래전 개발된 모델입니다. 선형 모델은 입력 특성에 대한 선형 함수를 만들어 예측을 수행합니다. 먼저 회귀의 선형 모델부터 알아보겠습니다
회귀의 선형 모델을 위한 일반화된 예측 함수는 다음과 같습니다.
𝑦̂ =𝑤[0]∗𝑥[0]+𝑤[1]∗𝑥[1]+...+𝑤[𝑝]∗𝑥[𝑝]+𝑏
위의 식에서 𝑥[0]부터 𝑥[𝑝]까지는 하나의 데이터 포인트에 대한 특성을 나타내고, (특성의 수는 𝑝+1 )와 𝑏는 모델이 학습해야 할 파라미터입니다. 𝑦̂ 는 모델이 만들어낸 예측값입니다.
그렇다면 특성이 한 개인 예측 함수는 어떻게 될까요? 다음과 같습니다.
𝑦̂ =𝑤[0]∗𝑥[0]+𝑏
위의 함수를 보면 예전 수학시간에 배운 직선의 방정식이 떠오릅니다. 𝑤[0]은 직선의 기울기( 계수(cofficient)라고도 합니다 )가 되고, 𝑏는 y 축과 만나는 절편( offset 또는 intercept )이 됩니다.
특성이 많아질수록 𝑤는 각 특성에 해당하는 기울기를 모두 가지게 됩니다. 즉 예측값은 입력특성에 𝑤의 가중치를 모두 더한 가중치의 합으로 볼 수 있겠습니다.
머신러닝에서 알고리즘이 주어진 데이터로부터 학습하는 파라미터라서 𝑤와 𝑏를 모델 파라미터라고 합니다.
나중에 살펴보겠지만 모델이 학습할 수 없어 사람이 직접 설정해 줘야 하는 파라미터를 하이퍼 파라미터(Hyper Parameter)라고 합니다.
wave 데이터셋을 이용해 눈으로 확인해 보겠습니다.
#필요 라이브러리 임포트
from IPython.display import display
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import mglearn
plt.rcParams['axes.unicode_minus'] = False
import platform
path = 'c:/Windows/Fonts/malgun.ttf'
from matplotlib import font_manager, rc
if platform.system() == 'Darwin':
rc('font', family='AppleGothic')
elif platform.system() == 'Windows':
font_name = font_manager.FontProperties(fname=path).get_name()
rc('font', family=font_name)
else:
print('Unknown system... sorry!')
# mglearn 샘플 그래프 보기
mglearn.plots.plot_linear_regression_wave()
그려진 그래프를 보면 직선의 방정식이 생각나는데요, 기울기는 대략 0.4, 절편은 0에 가깝게 나타나고 있는 것이 확인됩니다.
회귀 모델을 위한 선형 모델은 특성이 하나인 경우에는 직선, 두 개면 평면이 되며, 세 개 이상( 더 높은 차원 )이 되면 초평면(Hyperplane)이 되는 회귀 모델의 특징을 가지고 있습니다.
위의 그래프와 이전에 했었던 KNeighborsRegressor를 사용하여 만든 그래프를 비교해 보면 어떤가요? 직선을 지나는 점이 얼마 없는 것으로 보아 데이터의 상세정보를 대부분 잃어버린 것처럼 보이지 않나요?
사실 wave 같은 저 차원 데이터 셋에서는 타깃의 𝑦의 특성이 선형 조합이라고 생각하는 것은 매우 비현실 적인 가정입니다. 직선을 따라 데이터가 쭉 연결되지는 않으니까요.
하지만 1차원 데이터셋만 놓고 봐서 생긴 우리의 편견 일 수도 있습니다. 특성이 많은 데이터 셋이라면 선형 모델은 매우 훌륭한 성능을 발휘하며, 훈련 데이터보다 특성이 더 많은 경우엔 어떤 타깃 𝑦도 완벽하게 훈련 세트에 대해서 선형 함수로 모델링할 수 있습니다.
회귀를 위한 선형 모델은 다양합니다.
인기 있는 몇 가지 선형 모델을 살펴보려고 합니다. 이 모델들은 훈련 데이터로부터 모델 파라미터 𝑤와 𝑏를 학습하는 방법과 모델의 복잡도를 제어하는 방법에서 차이가 납니다.
선형 회귀 Linear Regression (최소제곱법)
선형 회귀(Linear Regression) 또는 최소 제곱법(OLS, Ordinary Least Squares)은 가장 간단하고 오래된 회귀용 선형 알고리즘이라고 할 수 있습니다.
선형 회귀는 훈련 세트에 있는 타깃 y 사이에 평균 제곱 오차(MSE - Mean Squared Error)를 최소화하는 모델 파라미터 𝑤와 𝑏를 찾습니다. 참고로 MSE는 다음과 같습니다.

위의 수식의 𝑛은 샘플의 개수입니다. 이를 𝐿2 norm을 적용했다라고 이야기 합니다.
위의 수식이 조금 불편 하긴 하지만 사실 MSE는 모델이 예측한 예측값( 𝑦𝑖^ )과 훈련 세트로 인해 훈련된 값 타깃값( 𝑦𝑖 )의 차이를 제곱하여 더한 후에 평균을 구한 것이라고 보면 됩니다. ( 샘플의 개수로 나눈 것 )
from sklearn.model_selection import train_test_split # 일반화 성능 평가를 위해 기존 데이터를 훈련 세트와 테스트 세트로 나눔
from sklearn.linear_model import LinearRegression
X, y = mglearn.datasets.make_wave(n_samples=60) # 60개의 샘플 데이터 준비
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42) # 훈련, 테스트 데이터셋 준비
lr = LinearRegression().fit(X_train, y_train) # 선형 회귀 모델에 훈련!모델이 데이터를 입력받고 훈련을 통해 알아내야 할 𝑤( 가중치 - weight 또는 계수 - cofficient )와 𝑏( 편향 - offset 또는 절편 - intercept ) 은 각각 coef와 intercept 변수에 들어 있습니다.
print("lr의 계수(weight 또는 cofficient) : {}".format(lr.coef_))
print("lr의 편향(offset 또는 intercept) : {}".format(lr.intercept_))
위의 결과에서 알 수 있는 사실 중 하나는 coef값은 NumPy 배열 형태이지만 intercept 값은 언제나 실수(float) 값 하나라는 사실입니다.
즉 coef 값은 각 특성 부여되는 가중치들의 배열이라는 사실을 알 수 있고, intercept 속성은 그 가중치에 대한 조정값이라는 점입니다.
wave 데이터 셋은 입력 특성이 하나밖에 없기 때문에 배열의 길이도 1이라는 사실을 알 수 있습니다.
print("훈련 세트 점수 : {}".format(lr.score(X_train,y_train)))
print("테스트 세트 점수 : {}".format(lr.score(X_test, y_test)))
단순히 선형 회귀(LinearRegression) 모델을 훈련시킨 후 점수를 확인해 보니 𝑅2 값이 66% 정도로 별로 좋지 않습니다. 또한 훈련 세트의 점수와 테스트 세트의 점수가 거의 비슷한 것을 확인할 수 있는데, 이는 과소적합인 상태를 의미합니다. 많이 생각할 필요 없이 우리가 테스트 용도로 사용한 wave 데이터 셋은 특성이 하나뿐인 1차원 데이터 셋이기 때문에 과대적합을 걱정하지 않아도 됩니다. 하지만 지금부터 사용해 볼 고차원 데이터 셋인 보스턴 주택 가격 데이터셋에 대해서는 선형 모델의 성능이 매우 높아지기 때문에 과대적합이 될 가능성이 있습니다!
X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 0)
lr = LinearRegression().fit(X_train, y_train)
print("훈련 세트 점수 : {:.2f}".format(lr.score(X_train, y_train)))
print("테스트 세트 점수 : {:.2f}".format(lr.score(X_test, y_test)))
테스트 결과 훈련 세트의 𝑅2는 95%지만, 테스트 세트의 점수는 61%입니다. 이는 모델이 과대적합되었다는 확실한 신호입니다. 따라서 우리는 모델의 일반화를 위해 복잡도를 제어할 수 있어야 하겠습니다. (각 특성별 가중치를 조절합니다.) 기본 선형 회귀 방식인 LinearRegression 모델로는 파라미터를 통해 복잡도를 제어 할 수 없으니, 여러 가지 회귀 모델을 알아보도록 하겠습니다.
릿지 Ridge 회귀
릿지(Ridge)도 회귀를 위한 선형 모델이므로 최소 제곱법 같은 예측 함수를 사용합니다. 릿지 회귀에서의 가중치(𝑤) 선택은 훈련 데이터를 잘 예측하기 위해서 뿐만 아니라 추가 제약 조건을 만족시키기 위한 목적도 있습니다. 즉 𝑤의 모든 원소가 0에 가깝게 만들어 가중치의 절댓값을 가능한 한 작게 한다는 뜻입니다. 결론적으로는 모든 특성이 예측(출력)에 주는 영향을 최소화하겠다는 뜻이 됩니다. 즉 𝑤에 의한 그래프의 기울기가 작아집니다. 이러한 제약 사향들을 규제(regularzation)이라고 합니다. 규제란 과대적합이 되지 않도록 모델을 강제로 제한한다는 뜻이 됩니다. 먼저 아무런 규제의 페널티가 없는 상황부터 살펴보겠습니다.
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train, y_train)
print("훈련 세트 점수 : {:.2f}".format(ridge.score(X_train, y_train)))
print("테스트 세트 점수 : {:.2f}".format(ridge.score(X_test, y_test)))
결과를 확인해 보니 훈련 세트에 대한 점수는 낮지만 테스트 세트에 대한 점수는 더 높네요. 선형 회귀(LinearRegression)는 보스턴 데이트 셋에 대해 과대적합 되지만 Ridge 회귀 방식은 더 자유로운 ( 특성에 제한이 걸리는 ) 모델이기 때문에 과대적합이 적어진다고 볼 수 있습니다.
따라서 모델의 적합도가 낮아졌다고 볼 수 있는데, 이렇게 모델의 복잡도가 낮아지면 훈련 세트에서의 성능은 나빠지지만 더욱 일반화된 모델이 됩니다.
우리는 테스트 세트에 대한 성능이기 때문에 보스턴 데이터셋에는 일반 선형 회귀보다는 Ridge 회귀가 어울리는 것 같네요
페널티
여기서 페널티에 대해 잠깐 이야기 하자면, 패널티란 예측 결과물에 대한 오차 범위 허용이라고 볼 수 있습니다. 이정도 오차는 괜찮아~ 라고 말 하는 것과 비슷합니다. 간단한 예로 택시의 예상 도착 시간을 예측 한다고 했을 때 예상 한 것 보다 1~2분 늦는 것은 별로가 문제가 되지 않으나, 10 ~ 20분 늦는 것은 예측이 매우 실패 했다 라고 판단 할 수 있습니다. 우리가 위에서 사용한 MSE(Mean Squad Error) 같은 공식이 예측값의 패널티에 대한 공식 같은 것이라고 판단하면 됩니다. MSE의 공식을 자세히 보면 오차 제곱( 타깃값 - 예측값의 제곱 )을 구하고 있는데, 이는 오차가 커지면 커질수록 더욱더 많은 페널티를 부여한다고 보면 됩니다. 보통 사용되는 다른 공식으로써 MAE(Mean Absolute Error)라는 것이 있습니다.
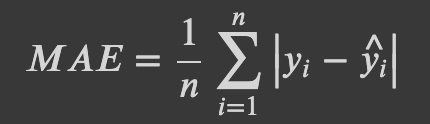
MSE와 다른 점은 MAE는 오차에 대한 페널티가 단순히 오차의 절대 값인 것을 확인할 수 있습니다. 이를 𝐿1 norm이라고 합니다. 즉 MSE는 오차가 커질수록 페널티가 커지고, MAE는 오차가 커질 수록 패널티가 일정 하다 라고 생각 해 볼 수 있겠습니다. 패널티를 계산하는 공식에는 RMSE, RMAE 등등의 여러가지 공식들이 있습니다.
Ridge 회귀에서의 패널티
Ridge는 모델을 단순하게 ( 계수 - 𝑤를 0에 가깝게 ) 해주고 훈련 세트와 테스트 세트 사이의 선능 사이를 절출 할 수 있는 방법을 제공합니다. 우리는 Ridge 회귀의 alpha 매개변수를 조절하여 모델의 성능을 단순화할 수 있습니다. 매개변수를 아무것도 넣지 않으면 alpha는 1.0을 기본적으로 사용하고 있었습니다. 참고로 alpha 값을 높이면 계수를 0으로 점점 가깝게 설정해 페널티의 효과가 커져 가중치가 차지하는 값이 0에 가까워져 모델이 단순해지고, alpha 값을 낮추면 점점 가중치가 높아져 모델이 복잡해집니다. Ridge 회귀를 사용할 때 최적화된 alpha 값은 사용하는 데이터셋에 따라 달라집니다. 바로 예를 들어 한번 보겠습니다. alpha 값을 10으로 조절한 경우입니다.
ridge10 = Ridge(alpha=10).fit(X_train, y_train)
print("훈련 세트 점수 : {:.2f}".format(ridge10.score(X_train, y_train)))
print("테스트 세트 점수 : {:.2f}".format(ridge10.score(X_test, y_test)))
alpha값을 10으로 높였더니 페널티의 효과가 높아져 가중치가 감소 한 것이 확인 됩니다. 즉 모델이 점점 단순화 되어 과소 적합 되어 가고 있다고 판단 할 수 있습니다.
이번엔 반대로 alpha 계수를 낮춰서 패널티의 효과를 줄이고 가중치를 증가시켜 보겠습니다.
ridge01 = Ridge(alpha=0.1).fit(X_train, y_train)
print("훈련 세트 점수 : {:.2f}".format(ridge01.score(X_train, y_train)))
print("테스트 세트 점수 : {:.2f}".format(ridge01.score(X_test, y_test)))
테스트 세트의 점수가 꽤나 높아졌습니다. 보스턴 주택가 데이터셋을 Ridge 회귀로 분석했을 때 alpha=0.1이 꽤나 좋은 성능을 내는 것 같네요.
이번엔 alpha 값에 따라서 각 모델의 coef_ ( 가중치 값 )이 어떻게 달라지는지 시각화해서 살펴보겠습니다.
예상을 해보자면 높은 alpha 값은 제약이 적은 모델이기 때문에 ( 가중치가 0에 점점 가까워지기 때문에 ) coef_의 절댓값의 크기가 작을 것 같네요. 확인해 보겠습니다.
plt.plot(ridge10.coef_, '^', label="Ridge alpha 10")
plt.plot(ridge.coef_, 's', label="Ridge alpha 1.0")
plt.plot(ridge01.coef_, 'v', label="Ridge alpha 0.1")
plt.plot(lr.coef_, 'o', label="LinearRegression")
plt.xlabel("계수 목록")
plt.ylabel("계수 크기")
plt.hlines(0, 0, len(lr.coef_))
plt.ylim(-25, 25)
plt.legend()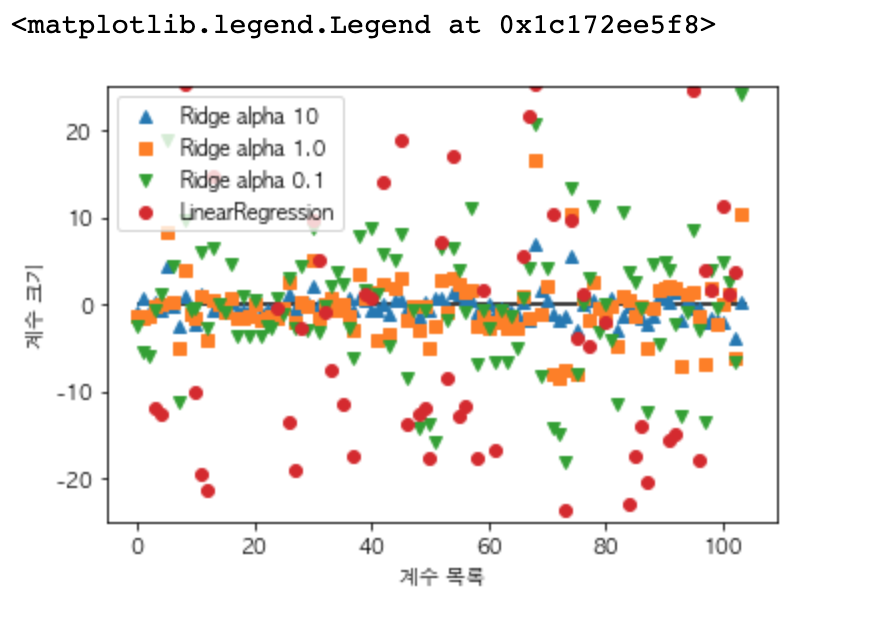
뭔가 굉장히 복잡해 보이네요, 먼저 X축은 coef_의 원소를 위치대로 나열한 것입니다. 즉 x=0은 첫 번째 특성, 약간 100을 넘는 값은 마지막 특성이라고 보면 될 것 같습니다.
y축은 계수의 수치를 나타내는데, alpha=10 일 때 ( 파란색 세모 ) 대부분의 계수는 -3부터 3 사이에 위치하는 것을 볼 수 있습니다. alpha=1 ( 주황색 네모 )의 계수의 크기는 조금 더 커져 가중치가 증가한 것이 확인됩니다. alpha=0.1 ( 초록색 세모 ) 같은 경우는 계수의 크기가 더 커져 가중치가 1일 때 보다 더 커진 것을 확인할 수 있고
alpha 값이 0인 ( 규제가 전혀 없는 ) LinearRegression 같은 경우는 그래프를 벗어나는 특성도 존재하는 것을 확인해 볼 수 있습니다.
Ridge에서 alpha 값은 고정되고, 데이터의 개수를 조절한다면?
규제의 효과를 확인해 보기 위해서 alpha를 1로 고정한 채로 훈련 데이터의 크기만 변화를 시켜 데이터 세트의 크기에 대해 훈련 효과를 확인해 보겠습니다.
보스턴 주택 가격 데이터세트에서 여러 가지 크기로 훈련시켜 LinearRegression과 Ridge(alpha=1)을 적용한 그래프를 확인 해 보겠습니다.
mglearn.plots.plot_ridge_n_samples()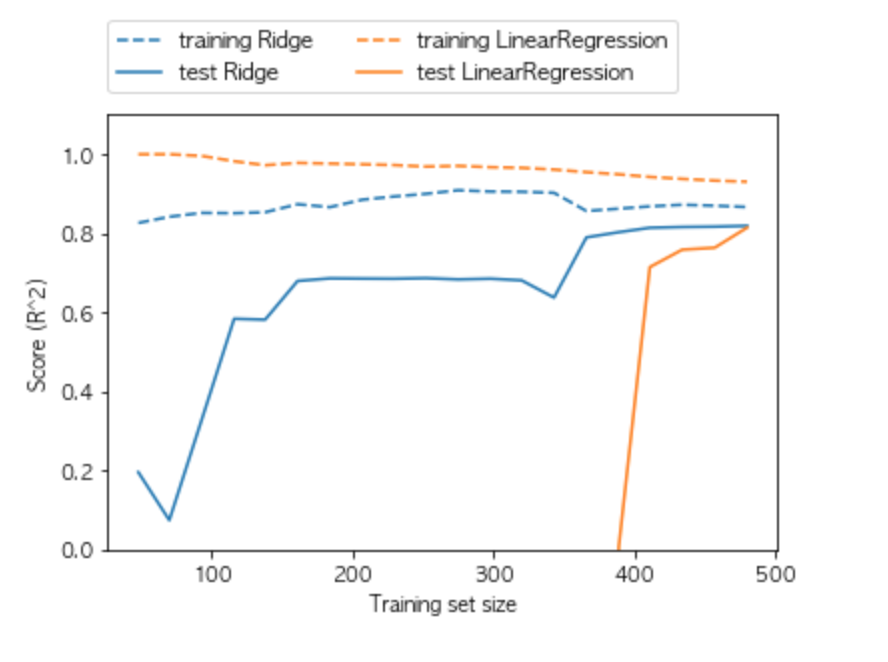
릿지와 선형 회귀 모두 훈련 세트의 점수 ( 점선 )가 테스트 세트의 점수 ( 실선 ) 보다 높은 것을 확인할 수 있습니다.
여기서 살펴볼 수 있는 사실은 릿지 회귀에는 규제가 적용되기 때문에 훈련 데이터의 점수가 대체적으로 선형 회귀보다 낮은 것을 확인할 수 있습니다. 이는 데이터 세트의 개수가 적으면 적을수록 더 확연히 확인해 볼 수 있습니다.
데이터 크기가 400 미만에서는 선형 회귀는 무엇도 학습하지 못하고 있는 것이 확인됩니다.
즉 두 모델의 성능은 ( 테스트 데이터세트의 결과 ) 데이터가 많으면 많을수록 좋아지며, 마지막에는 선형 회귀가 릿지 회귀의 테스트 점수를 따라잡는 것이 확인됩니다.
정리하자면 데이터를 충분히 주게 되면 규제 자체는 덜 중요해져 릿지 회귀와 선형 회귀의 성능이 같아질 것이라는 것을 예상해 볼 수 있다는 점입니다.
또 하나 이상한 점은 주황색 점선 ( 훈련 데이터셋 점수 )가 점점 내려가는 것을 확인할 수 있는데, 이는 선형 회귀의 훈련 데이터셋에 대한 성능이 점점 감소하는 것을 의미합니다.
이는 데이터가 많아지면 많아질수록 모델이 데이터를 기억하거나 과대적합 하기 어려워진다는 것을 의미합니다.
라쏘 Lasso 회귀
라쏘 회귀 방식도 릿지와 비슷하게 계수에 규제를 걸어 계수를 0에 가깝게 만들기 위한 노력을 합니다. 릿지 회귀와의 차이점은 릿지 회귀는 L2 규제 방식을 사용하는데 비해 라쏘 회귀는 L1 규제 방식을 사용하며, 실제 어떤 계수는 실제로 0이 되기도 한다는 점입니다.
계수가 0이 되면 해당 특성은 전혀 상관이 없이 완전히 제외된다는 뜻이 됩니다.
어떻게 보면 라쏘 회귀는 특성 선택( feature selection )이 자동으로 이루어진다고도 볼 수 있습니다.
일부 계수를 0으로 만들면 모델을 이해하기가 쉬워지고 이 모델의 가장 중요한 특성이 무엇인지가 드러납니다.
보스턴 주택가격 데이터셋에 라쏘를 적용시켜 보겠습니다.
from sklearn.linear_model import Lasso
lasso = Lasso().fit(X_train, y_train)
print("훈련 세트 점수 : {:.2f}".format(lasso.score(X_train, y_train)))
print("테스트 세트 점수 : {:.2f}".format(lasso.score(X_test, y_test)))
print("사용한 특성의 수 : {}".format(np.sum(lasso.coef_ != 0)))
확인 결과 라쏘는 훈련 세트와 테스트 세트의 점수가 전부 다 좋지 않습니다. 사용한 특성도 4개 정도밖에 안 되는 것으로 보아 과소적합이라고 생각할 수 있겠습니다.
릿지와 비슷하게 라쏘도 계수를 얼마나 강하게 보낼지를 조절하는 alpha 매개변수가 있습니다. 앞서 본 릿지에서는 기본적으로 alpha=1.0을 사용했었습니다.
과소적합을 줄이기 위해 alpha 값을 줄여보겠습니다. 하지만 이때 최대 반복 횟수를 의미하는 max_iter 값을 늘려 줘야 합니다.
max_iter는 내부적으로 Lasso의 학습 과정이 진행되는 최대 횟수를 의미합니다. 한 특성 씩 좌표축을 따라 최적화되는 좌표 하강법 방식을 사용하며 학습 과정이 max_iter에 지정된 횟수만큼 반복 횟수가 설정 되게 됩니다. lasso.niter를 이용해 반복 횟수를 확인할 수 있습니다.
lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train)
print("훈련 세트 점수 : {:.2f}".format(lasso001.score(X_train, y_train)))
print("테스트 세트 점수 : {:.2f}".format(lasso001.score(X_test, y_test)))
print("사용한 특성의 수 : {}".format(np.sum(lasso001.coef_ != 0)))
alpha 값을 줄여 봤더니 모델의 복잡도가 증가하여 훈련 세트와 테스트 세트의 점수가 모두 좋아졌습니다. 성능 자체가 릿지보다 조금 더 낫네요!
사용된 특성 자체가 105개 중 33개뿐이어서 모델을 분석하기가 쉬워진 것 같습니다.
하지만 alpha 값을 너무 낮추면 규제가 그만큼 효과가 없어지기 때문에 과대적합이 되므로 LinearRegression의 결과와 비슷해집니다.
lasso0001 = Lasso(alpha=0.0001, max_iter=1000000).fit(X_train, y_train)
print("훈련 세트 점수 : {:.2f}".format(lasso0001.score(X_train, y_train)))
print("테스트 세트 점수 : {:.2f}".format(lasso0001.score(X_test, y_test)))
print("사용한 특성의 수 : {}".format(np.sum(lasso0001.coef_ != 0)))
마찬가지로 alpha 값에 따른 다른 모델들의 계수를 그래프로 그려 보겠습니다.
plt.plot(lasso.coef_, 's', label="Lasso alpha=1")
plt.plot(lasso001.coef_, '^', label="Lasso alpha = 0.01")
plt.plot(lasso0001.coef_, 'v', label="Lasso alpha = 0.0001")
plt.plot(ridge01.coef_, 'o', label="Ridge alpha = 0.1")
plt.legend(ncol=2, loc=(0, 1.05))
plt.ylim(-25, 25)
plt.xlabel("계수 목록")
plt.ylabel("계수 크기")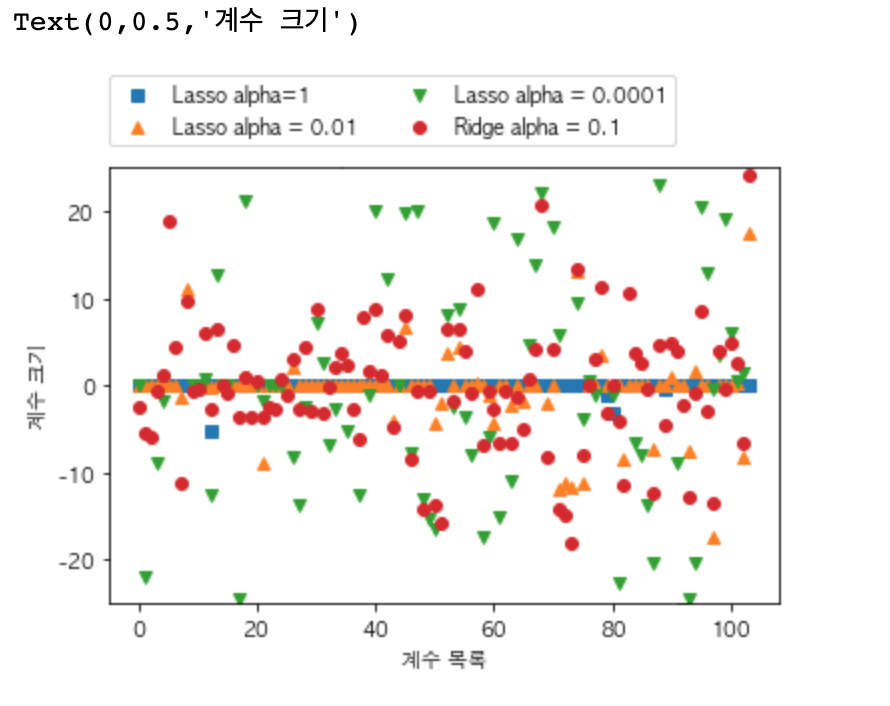
alpha가 1일 때( 파란색 )는 계수의 대부분이 0인 것을 알 수 있고, 나머지 계수들도 크기가 작다는 것이 확인됩니다. alpha를 0.01로 줄이면 ( 주황색 세모 ) alpha가 1일 때보다는 적지만 마찬가지로 계수 대부분이 1인 것이 확인 됩니다.
하지만 alpha 값이 0.0001이 되면 ( 초록색 세모 ) 계수 대부분이 0이 아니게 되고 그 값이 커지는 것이 확인 됩니다.
alpha 값이 0.1인 릿지 모델은 Lasso 모델과 비교해 성능은 비슷하지만 어떠한 계수도 0이 되지 않는 것이 확인 됩니다.
실제로 Lasso와 Ridge 중에서 릿지 회귀를 선호합니다.
하지만 입력 특성 자체가 많고 그중 일부분만 중요한 특성일 경우에는 Lasso가 더 좋은 선택이 될 수가 좋습니다. 또한 분석하기 쉬운 모델을 원한다면 Lasso가 일부 모델만 사용하므로 쉽게 해석할 수 있는 모델을 만들어 주게 될 수도 있습니다.
'Programming > 특성 공학' 카테고리의 다른 글
| [Machine Learning] 다중 선형 분류 (0) | 2023.05.16 |
|---|---|
| [Machine Learning] 선형 이진 분류 (0) | 2023.05.09 |
| [Machine Learning] 최근접 이웃(K-NN) (0) | 2023.04.24 |
| [Machine Learning]지도 학습의 종류 (0) | 2023.04.18 |
| [Machine Learning]지도 학습 (0) | 2023.04.14 |